Угловое ускорение характеризует изменение угловой скорости с течением времени. Если за промежуток времени ∆t = t1 - t угловая скорость изменяется на величину ∆$\omega $ = $\omega $1 - $\omega $, то числовое значение среднего углового ускорения за этот промежуток времени будет $\left\langle \varepsilon \right\rangle =\frac{\triangle \omega }{\triangle t}=\varepsilon $ . Перейдя к пределу при ∆t>0, получим: $\varepsilon ={\mathop{lim}_{\triangle t\to 0} \frac{\triangle \omega }{\triangle t}=\frac{d\omega }{dt}=\frac{d^2\varphi }{dt}=\dot{\omega }=\ddot{\varphi }\ }$.
Таким образом, числовое значение углового ускорения в данный момент времени равно первой производной от угловой скорости или второй производной от угла поворота по времени.
Размерность углового ускорения $1/T^2$ ($1/время^2$); в качестве единицы измерения обычно применяется $рад/с^2$ или, что то же, $1/с^2$ $(с^{-2})$.
Если модуль угловой скорости со временем возрастает, вращение тела называется ускоренным, а если убывает, замедленным. Легко видеть, что вращение будет ускоренным, когда величины $\omega $ и $\varepsilon $ имеют одинаковые знаки, и замедленным - когда знаки разные.
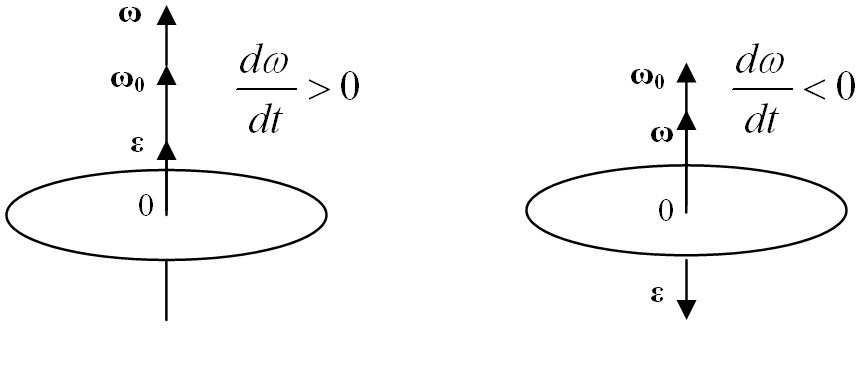
Рисунок 1. Вектор углового ускорения
Угловое ускорение тела можно представить в виде вектора $\overrightarrow{\varepsilon }=\frac{d\overrightarrow{\omega }}{dt}$ , направленного вдоль оси вращения. Направление $\overrightarrow{\varepsilon }$ совпадает с направлением $\overrightarrow{\omega }$, когда тело вращается ускоренно (рис.1, а), и противоположно $\overrightarrow{\omega }\ $при замедленном вращении (рис.1, б).
Если угловое ускорение тела во все время движения остается постоянным (${\mathbf \varepsilon }$=const), то вращение называется равнопеременным. Найдем закон равнопеременного вращения, считая, что в начальный момент времени $t_0$ угол ${\mathbf \varphi }$ = ${\mathbf \varphi }$0, а угловая скорость ${\mathbf \omega }$ = ${\mathbf \omega }$0 (${\mathbf \omega }$0 - начальная угловая скорость).
Из формулы $\varepsilon =\frac{d\omega }{dt}=\dot{\omega }=\ddot{\varphi }$ имеем d$\omega $ = $\varepsilon $dt. Интегрируя левую часть в пределах от $\omega_0$ до $\omega $, а правую - в пределах от 0 до t, найдем:
$\omega $ = $\omega_0$ + $\varepsilon $t, d$\varphi $ = $\omega $0dt + $\varepsilon tdt$.
Вторично интегрируя, найдем отсюда закон равнопеременного вращения: ${\mathbf \varphi }={\ {\mathbf \varphi }}_0\ +{\mathbf \omega }t+\frac{{\mathbf \varepsilon }t^2}{2}$
Если величины $\omega $ и $\varepsilon $ имеют одинаковые знаки, то вращение будет равноускоренным, а если разные - равнозамедленным.
Угловое ускорение связано с полным и тангенциальным. Для точки, неравномерно вращающейся по окружности радиуса R, $a_{\tau }=\varepsilon R$. Учитывая, что нормальное ускорение связано с угловой скоростью $a_n={\omega }^2R$, для полного ускорения получаем: $a=\sqrt{a^2_{\tau }+a^2_n}=R\sqrt{{\varepsilon }^2+{\omega }^4}$. В случае равнопеременного движения $\omega =\varepsilon t$, $a_n={\omega }^2R={\varepsilon }^2t^2R$, $a=R\sqrt{{{\varepsilon }^2+\varepsilon }^4t^4}=R\varepsilon \sqrt{1+{\varepsilon }^2t^4}$
На рис.2 показаны направления вращения гироскопа (волчка) и указано, увеличивается или уменьшается угловая скорость. Укажите номер рисунка, на котором правильно указано направление углового ускорения.
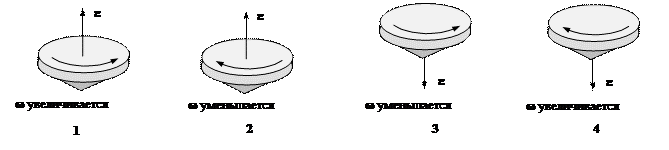
Рисунок 2
Решение
Псевдовектор угловой скорости связан с направлением вращения правилом буравчика (правого винта). На рис. 2.1 и рис. 2.3 он направлен вверх, на рис. 2.2 и рис. 2.4 - вниз.
При возрастании угловой скорости ее приращение, а соответственно и вектор углового ускорения совпадают с вектором угловой скорости (рисунки 1 и 4). При уменьшении угловой скорости ее приращение, а соответственно, и вектор углового ускорения противоположны вектору угловой скорости (рис.2 и рис.3). Следовательно, на всех рисунках направление углового ускорения указано правильно.
Материальная точка движется по окружности радиуса R так, что зависимость угла поворота от времени задана уравнением ${\mathbf \varphi }$=${\mathbf \alpha }$t3. Найти полное ускорение точки как функцию времени.
Решение
Найдём угловую скорость и угловое ускорение точки:
\[\omega =\frac{d\varphi }{dt}=3\alpha t^2;;\ \ \ \ \ \ \ \ \ \ \ \ \ \ \varepsilon =6\alpha t\]Полное ускорение
\[a=\sqrt{a^2_{\tau }+a^2_n}=R\sqrt{{\varepsilon }^2+{\omega }^4}=R\sqrt{36{\alpha }^2t^2+81{\alpha }^4t^8}=3\alpha tR\sqrt{4+9{\alpha }^2t^6}\]










