Физическое содержание тока смещения
Мы знаем, что постоянный ток в цепи с конденсатором не течет, переменный - протекает. Сила квазистационарного тока во всех элементах цепи, если они соединяются последовательно, одинакова. В конденсаторе, обкладки которого разделяет диэлектрик, ток проводимости, вызванный перемещением электронов, идти не может. Значит, если ток переменный (присутствует переменное электрическое поле), происходит некоторый процесс, который замыкает ток проводимости без переноса заряда между обкладками конденсатора. Этот процесс называют током смещения.
Любое переменное магнитное поле порождает вихревое электрическое поле. Исследуя разные электромагнитные процессы, Максвелл сделал вывод о том, что существует обратное явление: изменение электрического поля вызывает появление вихревого магнитного поля. Это одно из основных утверждений в теории Максвелла.
Так как магнитное поле -- обязательный признак любого тока, Максвелл назвал переменное электрическое поле током смещения. Ток смещения следует отличать от тока проводимости, который вызван движением заряженных частиц (электронов и ионов). Токи смещения появляются только в том случае, если электрическое смещение ($\overrightarrow{D}$) переменно. Объемная плотность тока смещения определяется как:
\[{\overrightarrow{j}}_{sm}=\frac{\partial \overrightarrow{D}}{\partial t}\left(1\right).\]Именно вследствие этого физическое содержание предположения Максвелла о токах смещения сводится к утверждению о том, что переменные электрические поля -- источники переменных магнитных полей.
Следует заметить, что плотность тока смещения определена производной вектора $\overrightarrow{D}$, а не самим вектором.
Ток смещения в диэлектрике
По определению вектора электрической индукции ($\overrightarrow{D}$):
где ${\varepsilon }_0$ -- электрическая постоянная, $\overrightarrow{E}$ -- вектор напряженность, $\overrightarrow{P}$ -- вектор поляризации. Следовательно, ток смещения можно записать как:
где величина $\frac{\partial \overrightarrow{P}}{\partial t}$ -- плотность тока поляризации. Токи поляризации -- токи, которые вызваны движением связанных зарядов, которые принципиально не отличаются от свободных зарядов. Поэтому нет ни чего странного, что токи поляризации порождают магнитное поле. Принципиальная новизна содержится в утверждении, что вторая часть тока смещения (${\varepsilon }_0\frac{\partial \overrightarrow{E}}{\partial t}$), не связанная с движением зарядов, также порождает магнитное поле. Получается, что в вакууме, любое изменение электрического поля по времени вызывает магнитное поле.
Однако, надо заметить, что сам термин «ток смещения» для диэлектриков имеет какое-то обоснование, так как в них действительно происходит смещение зарядов в атомах и молекулах. Но этот термин применяется и к вакууму, где зарядов нет, значит, нет их смещения.
Полный ток
В том случае, если в проводнике течет переменный ток, то внутри него имеется переменное электрическое поле. Значит, в проводнике существует ток проводимости ($j$) и ток смещения. Магнитное поле проводника определено суммой вышеназванных токов, то есть полным током ($\overrightarrow{j_p}$):
В зависимости от электропроводности вещества, частоты переменного тока, слагаемые в выражении (4), играют разную роль. В веществах с хорошей проводимостью (например, металлах) и при низких частотах переменного тока плотность тока смещения невелика, тогда как ток проводимости существенен. В таком случае, током смещения пренебрегают, в сравнении с током проводимости. В веществах с высоким сопротивлением (изоляторах) и при больших частотах тока ведущую роль играет ток смещения.
Оба слагаемых в выражении (4) могут иметь одинаковые знаки и противоположные. Следовательно, полный ток может быть и больше и меньше тока проводимости, может даже быть равен нулю.
Значит, в общем случае переменных токов магнитное поле определяется полным током. Если контур разомкнут, то на концах проводника обрывается только ток проводимости. В диэлектрике между концами проводника присутствует ток смещения, который замыкает ток проводимости. Получается, что если под электрическим током понимать полный ток, то в природе все токи замкнуты.
Задание: Плоский конденсатор заряжен и отключен от источника заряда. Он медленно разряжается объемными токами проводимости, которые появляются между обкладками, так как присутствует небольшая электрическая проводимость. Чему равна напряжённость магнитного поля внутри конденсатора? Считать, что краевых эффектов в конденсаторе нет.
Решение:
Допустим, что поверхностная плотность заряда на обкладках равна $\sigma \ и-\sigma .$ В таком случае, модуль вектора электрического смещения ($D$) для плоского конденсатора равен:
\[D=\sigma \left(1.1\right).\]Ток смещения можно найти как:
\[\overrightarrow{j_{sm}}=\frac{\partial \overrightarrow{D}}{\partial t}\ \left(1.2\right).\]Подставив вместо $D$ правую часть выражения (1.1), имеем:
\[j_{sm}=\frac{\partial \sigma }{\partial t}\left(1.3\right).\]В соответствии с законом сохранения заряда, можно записать, что:
\[j=-\frac{\partial \sigma }{\partial t}\left(1.4\right).\]Полный ток равен:
\[\overrightarrow{j_p}=\overrightarrow{j}+\overrightarrow{j_{sm}}\left(1.5\right).\]Для нашего плоского конденсатора, учитывая полученные выражения (1.3), (1.4), имеем:
\[j_p=\frac{\partial \sigma}{\partial t}-\frac{\partial \sigma}{\partial t}=0.\]Ответ: Магнитное поле в конденсаторе равно нулю.
Задание: Допустим, что неограниченную однородную проводящую среду поместили в металлический шар, имеющий заряд $Q$. В этой среде возникнут электрические токи, которые потекут в радиальных направлениях. Покажите, что данная ситуация требует введения тока смещения при описании возникающих полей.
Решение:
Электрические токи, которые текут от (или к ) шару, возбуждают магнитное поле. Определим направление вектора магнитной индукции этого магнитного поля.
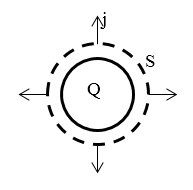
Рисунок 1.
Вектор $\overrightarrow{B}$ не имеет радиальной составляющей. Система обдает сферической симметрией. Если бы радиальная составляющая вектора индукции имелась, то она была бы одинаковой для всех точек сферы $S$ (рис.1), концентрической с поверхностью шара, имела направление от центра шара или к его центру. В обоих случаях поток вектора индукции через сферу $S$ был бы не равен нулю, что противоречит уравнению из системы Максвелла:
\[\oint\limits_S{\overrightarrow{B}d\overrightarrow{S}=0\left(2.1\right).}\]Значит, вектор индукции магнитного поля должен быть перпендикулярен к радиусу, который проведен из центра шара к рассматриваемой точке. Это также невозможно, так как все направления, перпендикулярные к радиусу, равноправны. Единственная возможность, которая не противоречит симметрии шара, заключается в том, что векторы $\overrightarrow{B}\ и\ \overrightarrow{H}$ всюду равны нулю. Следовательно, равна нулю плотность тока проводимости $\overrightarrow{j},\ $ что противоречит уравнению:
\[rot\overrightarrow{H}=\overrightarrow{j}\left(2.2\right).\]Для устранения полученного противоречия следует предположить, что магнитные поля порождаются не только токами проводимости. Добавим к току проводимости ток смещения ($I_{sm}$), который в нашем случае будет уничтожать возбуждаемое магнитное поле. Его величина определяется из условия:
\[I+I_{sm}=0\ \left(2.3\right).\]Ток проводимости, который течет от заряженного шара можно выразить как:
\[I=-\frac{dQ}{dt}\left(2.4\right).\]Из выражения (2.3) следует, что:
\[I_{sm}=\frac{dQ}{dt}\left(2.5\right).\]В соответствии с законом Кулона заряженного проводящего шара, имеем:
\[Q=4\pi r^2D\ \left(2.6\right).\]Найдем производную по времени от заряда, получим:
\[I_{sm}=4\pi r^2\frac{\partial D}{\partial t}\left(2.7\right).\]Плотность тока смещения при этом будет равна:
\[j_{sm}=\frac{I_{sm}}{S_{sf}}=\frac{4\pi r^2\frac{\partial D}{\partial t}}{4\pi r^2}=\frac{\partial D}{\partial t}.\]Полученное выражение совпадает с определением плотности тока смещения.












