Что такое тепловая машина
Термодинамика возникла как наука, основной задачей которой было создание наиболее эффективных тепловых машин.
Тепловой машиной (или тепловым двигателем) называется периодически действующий двигатель, который совершает работу за счет получения теплоты.
Обычно в тепловом двигателе механическая работа совершается газом при его расширении. При этом газ в тепловом двигателе называют рабочим телом. Очень часто в качестве рабочего тела выступают воздух или водяные пары. Расширение газа происходит в результате повышения его температуры и давления. Устройство, от которого рабочее тело получает тепло ($Q_n$), называют нагревателем. Таким образом, рабочее тело сначала расширяется от объема $V_1\ $до объема $V_2$ ${(V}_2>V_1)$, а затем сжимается до первоначального объема. Для того, чтобы работа, которая совершается за цикл, была больше нуля, давление и температура при расширении должны быть больше, чем при сжатии. Следовательно, рабочему телу при расширении теплоту сообщают, а при сжатии забирают. Значит, помимо нагревателя в тепловом двигателе присутствует еще и холодильник, которому рабочее тело тепло отдает. Рабочее тело совершает круговой процесс. Очевидно, что в этом процессе изменение внутренней энергии газа в двигателе равно нулю. Если в ходе расширения от нагревателя к рабочему телу передано $Q_n$- теплоты, при сжатии ${Q'}_{ch}$ теплоты рабочее тело передало холодильнику, исходя из первого начала термодинамики и учитывая, что $\triangle U=0$, получаем, что работа газа в круговом процессе равна:
\[A=Q_n-{Q'}_{ch}\ \left(1\right).\]Теплота ${Q'}_{ch}\ne 0$. Понятно, что чем лучше тепловой двигатель превращает теплоту, полученную от нагревателя в работу, тем такой двигатель выгоднее. Эффективность теплового двигателя характеризуют с помощью коэффициента полезного действия (КПД), который определен как:
\[\eta =\frac{A}{Q_n}\left(2\right).\]Уравнение (2), если учесть (1), можно записать в виде:
\[\eta =\frac{Q_n-{Q'}_{ch}}{Q_n}\left(3\right).\]КПД всегда $\eta
Машина, которая отбирает от тела с меньшей температурой некоторое количество теплоты $Q_{ch}$ и отдает телу с более высокой температурой количество тепла $Q_n'$, причем $Q_n'>Q_{ch}$, называется холодильной машиной. Над такой машиной должен быть совершена за цикл работа A'. Эффективность холодильной машины характеризуется ее холодильным коэффициентом (a), который вычисляется как:
\[a=\frac{Q_n'}{A'}=\frac{Q_n'}{Q'_n-Q_{ch}}\left(4\right).\]КПД необратимого теплового двигателя всегда меньше, чем того, который работает по обратимому циклу.
КПД теплового двигателя
Французский инженер Саади Карно установил важную зависимость КПД теплового двигателя от температуры нагревателя ($T_n$) и холодильника ($T_{ch}$). Независимо от конструкции теплового двигателя и выбора рабочего тела КПД идеальной тепловой машины определяется уравнением:
\[{\eta }_{max}=\frac{T_n-T_{ch}}{T_n}\left(5\right).\]Любой реальный тепловой двигатель может иметь КПД $\eta \le {\eta }_{max}$.
Идеальная машина, которую придумал Карно, работает по обратимому циклу, состоящему из двух изотерм (1-2, 4-3) и двух адиабат (2-3, 4-1) (рис.1). Рабочим телом в данном случае является идеальный газ. Мы помним, что адиабатный процесс идет без подвода и отвода тепла.
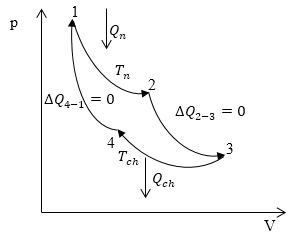
Рис. 1
На участке 1-2 рабочее тело получает от нагревателя с температурой $T_n$ количество тепла $Q_n$. В случае изотермического процесса мы можем записать, что:
\[Q_n=T_n\left(S_2-S_1\right)\left(6\right),\]где $S_1,\ S_2$- энтропии в соответствующих точках цикла на рис.1.
На участке 3-4 идеальный газ отдает тепло холодильнику с температурой $T_{ch}$, при этом количество теплоты, что эквивалентно получению газом теплоты ${-Q}_{ch}$, соответственно:
\[{-Q}_{ch}=T_{ch}\left(S_1-S_2\right)\left(7\right).\]В скобках выражения (7) указано приращение энтропии в процессе 3-4.
Подставим формулы (6), (7) в определение КПД теплового двигателя, получим:
\[\eta =\frac{T_n\left(S_2-S_1\right)+T_{ch}\left(S_1-S_2\right)}{T_n\left(S_2-S_1\right)}=\frac{T_n-T_{ch}}{T_n}\left(8\right).\]И в нашем выводе уравнения (8) не делалось никаких предположений о свойствах рабочего тела и устройстве теплового двигателя.
Уравнение (8) показывает, что для повышения КПД необходимо повышать $T_n$ и понижать $T_{ch}.$ Но так как абсолютный ноль недостижим, то единственный путь увеличить КПД теплового двигателя, увеличивать $T_n$.
Задача по созданию теплового двигателя, который совершал бы работу без холодильника, кажется весьма интересной. В физике такая машина называется вечным двигателем второго рода. Она в принципе не противоречит первому закону термодинамики. Однако эта проблема также неразрешима, как и создание вечного двигателя первого рода. Этот опытный факт в термодинамике принят как постулат -- второе начало термодинамики.
Задание: Рассчитайте КПД теплового двигателя с температурой нагревателя 1000С и температурой холодильника 00С. Тепловую машину считайте идеальной.
Решение:
Используем для решения, выражение для КПД теплового двигателя в виде:
\[\eta =\frac{T_n-T_{ch}}{T_n}.\]Переведем температуры в СИ, то есть:
\[T_n={100}^0С+273=373\ (К)\] \[T_{ch}=0^0С+273=273\ (К)\]Подставим данные для расчета, проведем вычисления:
\[\eta =\frac{373-273}{373}=0.27=27\%.\]Ответ: КПД теплового двигателя 27%.
Задание: Найти КПД цикла, который представлен на рис. 2, если в пределах цикла объем идеального газа изменяется в n раз. Рабочим веществом является газ с показателем адиабаты $\gamma$.
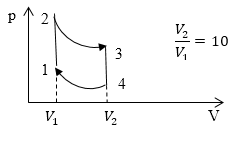
Рис. 2
В качестве основания для расчета КПД используем формулу:
\[\eta =\frac{Q_n-{Q'}_{ch}}{Q_n}\left(2.1\right).\]Процесс, в котором газ получает тепло -- это процесс 1-2 ($Q_{12}=Q_n$):
\[Q_{12}=\triangle U_{12}+A_{12}\left(2.2\right),\]где $A_{12}=0$ так как это изохорный процесс. Следовательно:
\[Q_{12}=\triangle U_{12}=\frac{i}{2}\nu R\left(T_2-T_1\right)\left(2.3\right).\]Процесс, в котором газ тепло отдает -- это процесс 3-4 изохорный, (${{-Q}}_{34}={Q'}_{ch}$). Следовательно:
\[Q_{34}=\triangle U_{34}=\frac{i}{2}\nu R\left(T_4-T_3\right)\left(2.4\right).\]Адиабатные процессы идут без подвода и отвода тепла.
Подставим полученные количества теплоты в выражение для КПД, имеем:
\[\eta =\frac{\frac{i}{2}\nu R\left(T_2-T_1\right)+\frac{i}{2}\nu R\left(T_4-T_3\right)}{\frac{i}{2}\nu R\left(T_2-T_1\right)}=\frac{T_2-T_1+T_4-T_3}{T_2-T_1}=1-\frac{T_3-T_4}{T_2-T_1}\ \left(2.5\right).\]Используем уравнение для адиабаты для процесса 2-3:
\[T_2V^{\gamma -1}_1=T_3V^{\gamma -1}_2\to T_2=T_3\frac{V^{\gamma -1}_2}{V^{\gamma -1}_1}=T_3n^{\gamma -1}\left(2.6\right).\]Используем уравнение для адиабаты для процесса 4-1:
\[T_1V^{\gamma -1}_1=T_1V^{\gamma -1}_2\to T_1=T_4\frac{V^{\gamma -1}_2}{V^{\gamma -1}_1}=T_4n^{\gamma -1}\left(2.7\right).\]Найдем разность температур $T_2-T_1$:
\[T_2-T_1=\left({T_3-T}_4\right)n^{г-1}\left(2.8\right).\]Подставим в (2.5) разность температур из (2.8), получим:
\[\eta =1-\frac{T_3-T_4}{\left({T_3-T}_4\right)n^{\gamma -1}}=1-\frac{1}{n^{\gamma -1}}=1-n^{1-\gamma }\left(2.9\right).\]Ответ: КПД цикла $\eta =1-n^{1-г}$.











