Что такое адиабатический процесс
Адиабатическим или адиабатным процессом называют процесс, при котором отсутствует теплообмен с окружающей средой ($\delta Q=0$).
В таком случае первое начало термодинамики можно записать в виде:
\[0=\frac{i}{2}\nu RdT+pdV\ \left(1\right).\]Из уравнения (1) следует, что при увеличении объема в адиабатном процессе уменьшается температура системы. Или говорят, что в адиабатном процессе работа совершается за счет уменьшения внутренней энергии системы. И обратное справедливо: работа, совершенная над системой, увеличивает внутреннюю энергию системы и, как следствие, температуру. Уравнение, которое характеризует адиабатный процесс в термодинамических параметрах (уравнение адиабаты) носит имя Пуассона. Получим это уравнение для идеального газа. Из уравнения состояния идеального газа:
\[pV=\nu RT\to T=\frac{pV}{\nu R}\left(2\right).\]Из соотношения Майера:
\[C_p-C_V=\nu R\ \left(3\right).\]Подставим (3) в (2), получим:
\[T=\frac{pV}{C_p-C_V}\to p=\frac{T(C_p-C_V)}{V}\ \left(4\right).\]Разделим уравнение (1) $C_VT\ (\ C_V=\frac{i}{2}нR)$, получим:
\[0=C_V\frac{dT}{T}+\frac{(C_p-C_V)}{VC_V}dV\to \frac{dT}{T}+\left(\gamma -1\right)\frac{dV}{V}=0\to \frac{dT}{T}=\left(1-\gamma \right)\frac{dV}{V}\left(5\right),\]где $\gamma =\frac{C_p}{C_V}$ -- показатель адиабаты. Проинтегрируем уравнение (5):
\[{ln T={ln V^{1-\gamma }+lnA\ }\ }\left(6\right),\]где $lnA$- некоторая постоянная.
Потенцируем уравнение (6), получаем:
\[{ln T={ln AV^{1-\gamma }\ }\ }.\] \[{T V^{\gamma -1}=А=const\ }\left(7\right).\]Уравнение (7) есть уравнение адиабаты в параметрах T,V. Для того, чтобы перейти к уравнению адиабаты, в параметрах p,V используют уравнение Менделеева -- Клайперона. И получают уравнение адиабаты в виде:
\[{p V^{\gamma }=const\ }\ \left(8\right).\]Или в параметрах p,T уравнение (7,8) имеет вид:
\[{T^{\gamma } p^{1-\gamma }=const\ \left(9\right).\ }\]Зная, что теплоемкости можно представить как:
\[с_{\mu p}=\frac{i+2}{2}R,\ с_{\mu V}=\frac{i}{2}R\ \left(10\right).\]показатель адиабаты исходя из ($\gamma =\frac{C_p}{C_V}$) и уравнений (10)
\[\gamma =\frac{i+2}{i}\ \left(11\right).\]Легко получить формулу работы для адиабатного процесса. По определению работа газа A равна:
\[A=\int\limits^{V_2}_{V_1}{pdV}=p_1V^{\gamma }_1\int\limits^{V_2}_{V_1}{\frac{dV}{V^{\gamma }}}=\frac{p_1V^{\gamma }_1}{1-\gamma }\left(V^{1-\gamma }_2-V^{1-\gamma }_1\right)=\frac{\nu RT_1}{\gamma -1}\left[1-{\left(\frac{V_1}{V_2}\right)}^{\gamma -1}\right]\ \left(12\right),\]где $p_1V_1=\nu RT_1.$ Используя уравнение адиабаты, записанное для двух состояний в параметрах $V,T$, получаем:
\[A=\nu R\frac{\left(T_1-T_2\right)}{\gamma -1}\ \left(13\right).\]Что такое адиабата
Линия, изображающая на термодинамической диаграмме адиабатный процесс, называется адиабатой (рис.1).
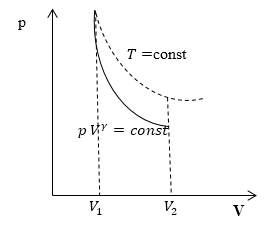
Рис. 1
Для сравнения на рис. 1 представлена также изотерма (пунктиром). На рис. 1 видно, что адиабата идет круче, чем изотерма. Работа в адиабатическом процессе по расширению от объема $V_1\ $до $V_2$ меньше, чем в изотермическом процессе с таким же изменением объема. Это объясняется тем, что при адиабатном процессе происходит охлаждение газа. В изотермическом процессе при расширении давление уменьшается только за счет уменьшения плотности, тогда как в адиабатном за счет плотности и средней кинетической энергии молекул (соответственно температуры).
Задание: Одноатомный газ совершает адиабатное расширение от объема $V_1=$1$м^3\ $при температуре $Т_1=400\ К$, при этом давление газа изменяется от $p_1=5\cdot {10}^6Па\ $до $p_2=2\cdot {10}^6\ Па$. Найдите объем газа в конечном состоянии.
Решение:
При адиабатном расширении имеем:
\[{p_1 {V_1}^{\gamma }=p_2\ }{V_2}^{\gamma }\ \left(1.1\right),\]где $\gamma =\frac{i+2}{i}\ ,\ $так как газ одноатомный, то i=3, следовательно, $\gamma =\frac{3+2}{3}=\frac{5}{3}$. Значит можно выразить интересующий нас объем:
\[V_2={\left(\frac{p_1}{p_2}\right)}^{\frac{1}{\gamma }}V_1\ \left(1.2\right).\]Проведем вычисления:
\[V_2={\left(\frac{5}{2}\right)}^{\frac{3}{5}}1=4,6\ (м^3)\]Ответ: Объем газа в конечном состоянии 4,6 $м^3.$
Задание: Некоторую массу газа сжали так, что $\frac{V_1}{V_2}=5$, в первом случае процесс проводился адиабатический, второй изотермический. Начальные состояния газов одинаковы в том и другом случае. Найти отношение работ $\frac{A_1}{A_2}=?$
Решение:
Работа в адиабатном процессе задана формулой над газом:
\[A_1=-\frac{\nu RT_1}{\gamma -1}\left[1-{\left(\frac{V_1}{V_2}\right)}^{\gamma -1}\right]\left(2.1\right).\]Формула для работы в изотермическом процессе имеет вид:
\[A_2=-\nu RT_1ln\left(\frac{V_2}{V_1}\right)\left(2.2\right).\]Тогда найдем искомое отношение:
\[\frac{A_1}{A_2}=\frac{\frac{\nu RT_1}{\gamma -1}\left[1-{\left(\frac{V_1}{V_2}\right)}^{\gamma -1}\right]}{\nu RT_1ln\left(\frac{V_2}{V_1}\right)}=\frac{1-{\left(\frac{V_1}{V_2}\right)}^{\gamma -1}}{(-\gamma +1)ln\left(\frac{V_1}{V_2}\right)}\ \left(2.3\right).\]Для коэффициента адиабаты мы знаем формулу вычисления через число степеней свободы$(i)$, а для одноатомного газа $i=3$:
\[\gamma =\frac{i+2}{i}\ \left(2.4\right).\]Подставим данные из условий задачи, получим:
\[\frac{A_1}{A_2}=\frac{1-{\left(5\right)}^{\frac{2}{3}}}{-\frac{2}{3}{ln \left(5\right)\ }}=\frac{-1,9}{-1,07}=1,89\]Ответ: Отношение работ, которые совершают над газом в процессах сжатия в адиабатном процессе и изотермическом равно 1,89. Работа над газом в адиабатном процессе больше.











