Равновесием тела называют такое состояние, когда любое ускорение тела равняется нулю, то есть все действия на тело сил и моментов сил уравновешены. При этом тело может:
- находиться в состоянии спокойствия;
- двигаться равномерно и прямолинейно;
- равномерно вращаться вокруг оси, которая проходит через центр его тяжести.
Условия равновесия тела
Если тело находится в равновесии, то одновременно выполняются два условия.
- Векторная сумма всех сил, действующих на тело, равна нулевому вектору: $\sum_n{{\overrightarrow{F}}_n}=\overrightarrow{0}$
- Алгебраическая сумма всех моментов сил, действующих на тело, равна нулю: $\sum_n{M_n}=0$
Два условия равновесия являются необходимыми, но не являются достаточными. Приведем пример. Рассмотрим равномерно катящееся без проскальзывания колесо по горизонтальной поверхности. Оба условия равновесия выполняются, однако тело движется.
Рассмотрим случай, когда тело не вращается. Для того, чтобы тело не вращалось и находилось в равновесии, необходимо, чтобы сумма проекций всех сил на произвольную ось равнялась нулю, то есть равнодействующая сил . Тогда тело или находится в спокойствии, или двигается равномерно и прямолинейно.
Тело, которое имеет ось вращения, будет находиться в равновесном состоянии, если выполняется правило моментов сил: сумма моментов сил, которые вращают тело по часовой стрелке, должна равняться сумме моментов сил, которые вращают его против часовой стрелки.
Чтобы получить нужный момент при наименьшем усилии, нужно прикладывать силу как можно дальше от оси вращения, увеличивая тем же плечо силы и соответственно уменьшая значение силы. Примеры тел, которые имеют ось вращения, : рычаг, двери, блоки, коловорот и тому подобное.
Три вида равновесия тел, которые имеют точку опоры
- стойкое равновесие, если тело, будучи выведенным из положения равновесия в соседнее ближайшее положение и оставлено в спокойствии, вернется в это положение;
- неустойчивое равновесие, если тело, будучи выведенным из положения равновесия в соседнее положение и оставлено в спокойствии, будет еще больше отклоняться от этого положения;
- безразличное равновесие - если тело, будучи выведенным в соседнее положение и оставлено в спокойствии, останется в новом своем положении.
Равновесие тела с закрепленной осью вращения
- стойким, если в положении равновесия центр тяжести С занимает самое низкое положение из всех возможных ближних положений, а его потенциальная энергия будет иметь наименьшее значение из всех возможных значений в соседних положениях;
- неустойчивым, если центр тяжести С занимает наивысший из всех ближних положений, а потенциальная энергия имеет наибольшее значение;
- безразличным, если центр тяжести тела С во всех ближних возможных положениях находится на одном уровне, а потенциальная энергия при переходе тела, не изменяется.
Тело A массой m = 8 кг поставлено на шероховатую горизонтальную поверхность стола. К телу привязана нить, перекинутая через блок B (рисунок 1, а). Какой груз F можно подвязать к концу нити, свешивающейся с блока, чтобы не нарушить равновесия тела A? Коэффициент трения f = 0,4; трением на блоке пренебречь.
Решение
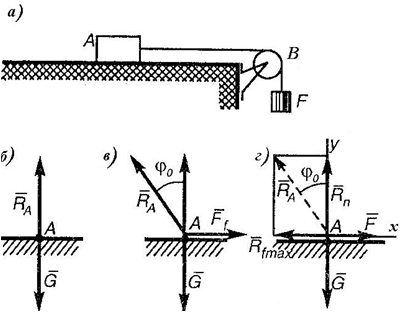
Рисунок 1.
Определим вес тела ~A: ~G = mg = 8$\cdot $9,81 = 78,5 Н.
Считаем, что все силы приложены к телу A. Когда тело поставлено на горизонтальную поверхность, то на него действуют только две силы: вес G и противоположно направленная реакция опоры RA (рис. 1, б).
Если же приложить некоторую силу F, действующую вдоль горизонтальной поверхности, то реакция RA, уравновешивающая силы G и F, начнет отклоняться от вертикали, но тело A будет находиться в равновесии до тех пор, пока модуль силы F не превысит максимального значения силы трения Rf max, соответствующей предельному значению угла ${\mathbf \varphi }$o(рис. 1, в).
Разложив реакцию RA на две составляющие Rf max и Rn, получаем систему четырех сил, приложенных к одной точке (рис. 1, г). Спроецировав эту систему сил на оси x и y, получим два уравнения равновесия:
${\mathbf \Sigma }Fkx = 0, F - Rf max = 0$;
${\mathbf \Sigma }Fky = 0, Rn - G = 0$.
Решаем полученную систему уравнений: F = Rf max, но Rf max = f$\cdot $ Rn, а Rn = G, поэтому F = f$\cdot $ G = 0,4$\cdot $ 78,5 = 31,4 Н; m = F/g = 31,4/9,81 = 3,2 кг.
Ответ: Масса груза т = 3,2 кг
Система тел, изображённая на рис.2, находится в состоянии равновесия. Масса груза тг=6 кг. Угол между векторами $\widehat{{\overrightarrow{F}}_1{\overrightarrow{F}}_2}=60{}^\circ $. $\left|{\overrightarrow{F}}_1\right|=\left|{\overrightarrow{F}}_2\right|=F$. Найти массу гирь.
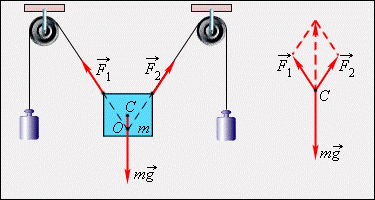
Рисунок 2.
Решение
Равнодействующая сил ${\overrightarrow{F}}_1и\ {\overrightarrow{F}}_2$ равна по модулю весу груза и противоположна ему по направлению: $\overrightarrow{R}={\overrightarrow{F}}_1+{\overrightarrow{F}}_2=\ -m\overrightarrow{g}$. По теореме косинусов, ${\left|\overrightarrow{R}\right|}^2={\left|{\overrightarrow{F}}_1\right|}^2+{\left|{\overrightarrow{F}}_2\right|}^2+2\left|{\overrightarrow{F}}_1\right|\left|{\overrightarrow{F}}_2\right|{cos \widehat{{\overrightarrow{F}}_1{\overrightarrow{F}}_2}\ }$.
Отсюда ${\left(mg\right)}^2=$; $F=\frac{mg}{\sqrt{2\left(1+{cos 60{}^\circ \ }\right)}}$;
Поскольку блоки подвижные, то $m_г=\frac{2F}{g}=\frac{2m}{\sqrt{2\left(1+\frac{1}{2}\right)}}=\frac{2\cdot 6}{\sqrt{3}}=6,93\ кг\ $
Ответ: масса каждой из гирь равна 6,93 кг











