Рычаг

Человечество использует рычаг с доисторических времён. Принцип его действия был понят людьми интуитивно на основании опыта. Рычаги широко применялись в античном мире - для перемещения тяжестей, подъёма грузов.

Рисунок 1. Применение рычага в античном мире

Рычаг - это не обязательно длинный и тонкий предмет. Например, рычагом является любое колесо, так как оно может вращаться вокруг оси.

Первое научное описание принципа действия рычага дал Архимед, и оно практически в неизменном виде применяется до сих пор. Основные понятия, используемые для описания принципа действия рычага - линия действия силы и плечо силы.

Линией действия силы называют прямую, проходящую через вектор силы. Плечом силы называют кратчайшее расстояние от оси рычага или точки опоры до линии действия силы.

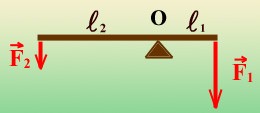
Рисунок 2. Линия действия силы и плечо силы

На рис. 2 линии действия сил $F_1$ и $F_2$ задаются их направляющими векторами, а плечи этих сил -- перпендикулярами $l_1$ и $l_2$, проведенными от оси вращения O к линиям приложения сил.

Равновесие рычага наступает при условии, что отношение приложенных к его концам параллельных сил обратно отношению плеч и моменты этих сил противоположны по знаку:

Следовательно, рычаг, как и все простые механизмы, подчиняется «золотому правилу механики», согласно которому выигрыш в силе пропорционален проигрышу в перемещении.

Условие равновесия можно записать и в другой форме:

Произведение силы, вращающей рычаг, на плечо этой силы называется моментом силы. Момент силы - физическая величина и может быть измерена, ее единица измерения - ньютоно-метр ($Н\cdot м$).

Все рычаги могут быть разделены на три класса, отличающиеся относительными положениями усилия, нагрузки и точки опоры.

Наиболее распространенным типом рычага является рычаг первого класса, у которого точка опоры (ось вращения) лежит между точками приложения сил (рис.3). Рычаги первого класса имеют много разновидностей, используемых нами в повседневной жизни, например плоскогубцы, гвоздодер, ножницы и т.д.

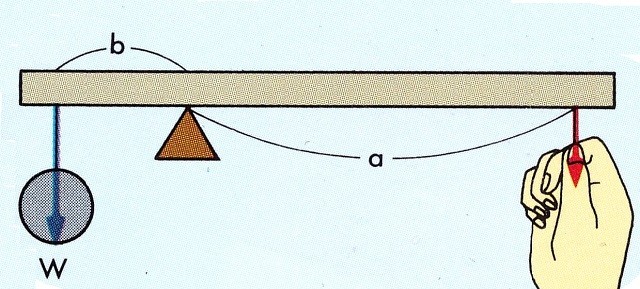
Рисунок 3. Рычаг 1 класса

Рычагом первого класса также является педаль (рис.4). Ось её вращения проходит через точку О. К педали приложены две силы: $F_1$ - сила, с которой нога давит на педаль, и $F_2$ - сила упругости натянутого троса, прикреплённого к педали. Проведя через вектор ${\overrightarrow{F}}_1$ линию действия силы (изображена пунктиром), и, построив к ней перпендикуляр из т.О, мы получим отрезок ОА - плечо силы $F_1$.

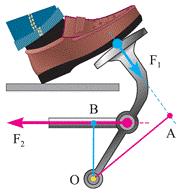
Рисунок 4. Педаль как пример рычага 1 рода

С силой $F_2$ дело обстоит проще: линию её действия можно не проводить, так как её вектор расположен более удачно. Построив из т. О перпендикуляр на линию действия силы $F_2$, получим отрезок ОВ - плечо силы $F_2$.

У рычагов второго и третьего класса точки приложения сил находятся по одну сторону от оси вращения (точки опоры). Если ближе к опоре находится нагрузка - это рычаг второго класса (рис.5).

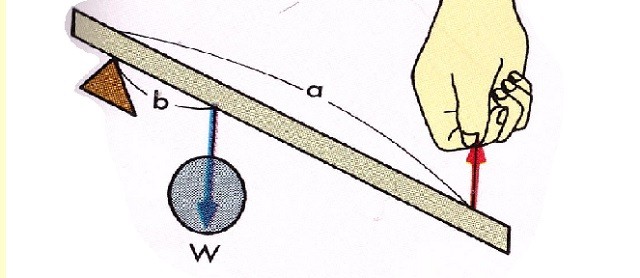
Рисунок 5. Рычаг 2 класса

Тачка, открывалка для бутылок, степлер и дырокол относятся к рычагам второго класса, которые всегда увеличивают приложенное усилие.

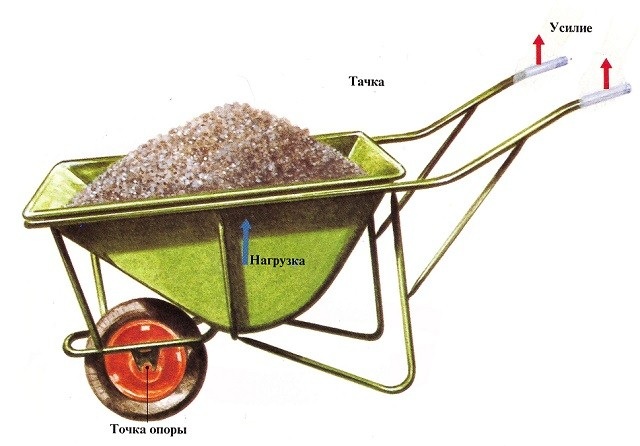
Рисунок 6. Тачка как пример рычага 2 класса

Если точка приложения силы ближе к оси вращения, чем нагрузка - это рычаг третьего класса (рис.7).

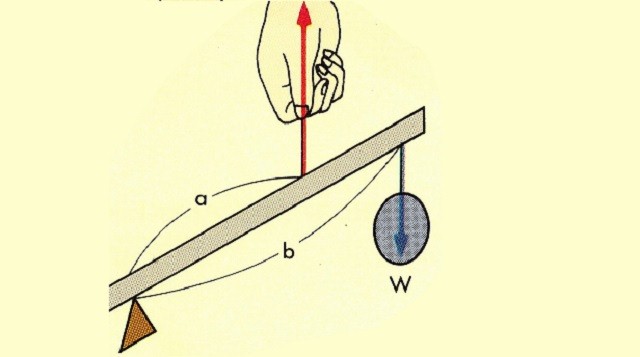
Рисунок 7. Рычаг 3 класса

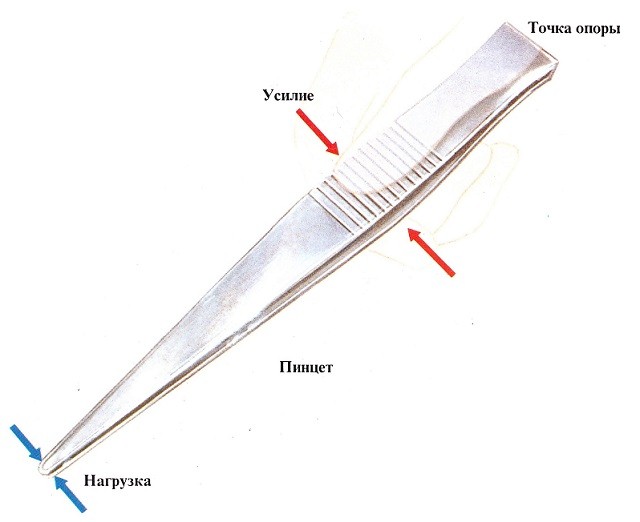
Например, пинцет представляет собой два рычага третьего класса, соединённые в точке опоры.