Всякое тело под влиянием сил, действующих со стороны других тел, вообще говоря, испытывает ускорение; в частности, покоящееся тело приходит в движение. Однако в некоторых случаях тело, находящееся под действием нескольких сил, все же может оставаться в покое. Так, если на покоящееся тело действуют одновременно две силы, равные по величине и направленные по одной прямой в противоположные стороны, то тело не испытывает ускорений и может оставаться в покое. В других случаях условия покоя тела при действии на него сил оказываются более сложными. Изучение этих условий, т. е. условий равновесия тел (или, иначе, условий равновесия сил), и составляет задачу статики.
Таким образом, статика прежде всего позволяет определить условия равновесия всех разнообразнейших сооружений, которые мы создаем: зданий, мостов, арок, подъемных кранов и т. д. Но этим не исчерпывается практическое значение статики. Статика позволяет дать ответ и на некоторые вопросы, касающиеся движения тел.
Статика - самый старый раздел механики; некоторые из ее принципов были известны уже древним египтянам и вавилонянам, о чем свидетельствуют построенные ими пирамиды и храмы. Среди первых создателей теоретической статики был Архимед (ок. 287-212 до н.э.), который разработал теорию рычага и сформулировал основной закон гидростатики. Родоначальником современной статики стал голландец С. Стевин (1548-1620), который в 1586 сформулировал закон сложения сил, или правило параллелограмма, и применил его в решении ряда задач.
Законы статики вытекают из общих законов динамики как частный случай, когда скорости твердых тел стремятся к нулю, но по историческим причинам и педагогическим соображениям статику часто излагают независимо от динамики, строя ее на следующих постулируемых законах и принципах:
- законе сложения сил,
- принципе равновесия и
- принципе действия и противодействия.
В случае твердых тел (точнее, идеально твердых тел, которые не деформируются под действием сил) вводится еще один принцип, основанный на определении твердого тела. Это принцип переносимости силы: состояние твердого тела не изменяется при перемещении точки приложения силы вдоль линии ее действия.
В основе статики лежит система аксиом - экспериментально установленных истин, из которых выводятся все остальные законы статики.
Две силы, приложенные к абсолютно твердому телу, будут уравновешены (эквивалентны нулю) тогда и только тогда, когда они равны по модулю, действуют по одной прямой и направлены в противоположные стороны (рис.1).
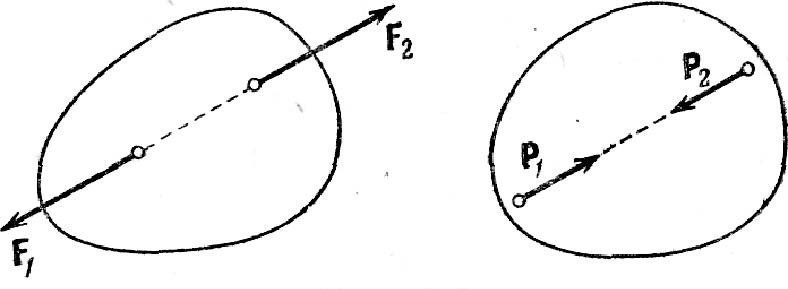
Рисунок 1.
Примеры уравновешивания сил
Не нарушая состояния абсолютно твердого тела, к нему можно прикладывать или отбрасывать силы тогда и только тогда, когда они составляют уравновешенную систему, в частности, если эта система состоит из двух сил, равных по модулю, действующих по одной прямой и направленных в противоположные стороны.
Из аксиомы 2 вытекает следствие: не нарушая состояния тела, точку приложения силы можно переносить вдоль линии ее действия (рис.2).
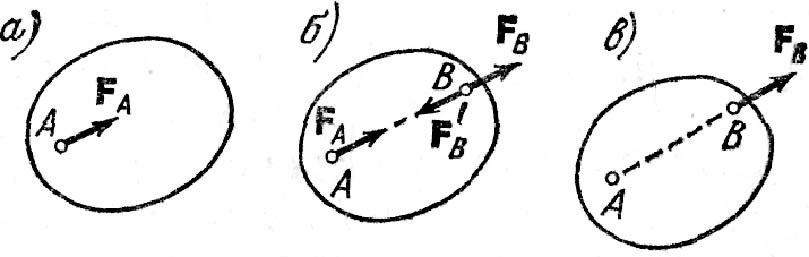
Рисунок 2.
Точку приложения силы можно переносить вдоль линии её действия путём добавления системы уравновешивающих друг друга сил
Не меняя состояния тела, две силы, приложенные к одной его точке, можно заменить одной равнодействующей силой, приложенной в той же точке и равной их геометрической сумме (рис. 3).
Рисунок 3.
Равнодействующая системы сил, приложенных к одной точке
Силы взаимодействия двух тел равны по модулю и направлены по одной прямой в противоположные стороны.
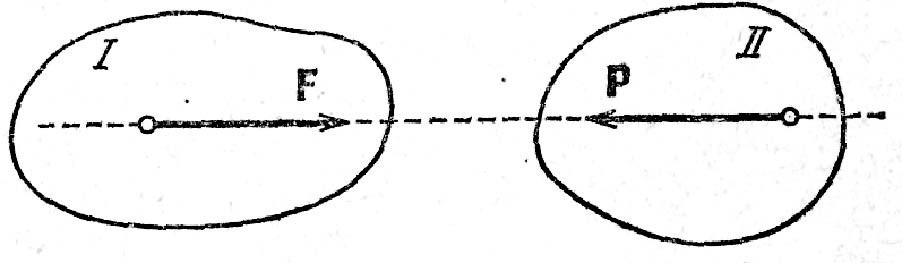
Рисунок 4.
Если тело I действует на тело II с силой Р, а тело II действует на тело I с силой F (рис. 4), то эти силы равны по модулю (F = Р) и направлены по одной прямой в противоположные стороны, т. е. F = - Р.
Равновесие деформируемого тела не нарушится, если жестко связать его точки и считать тело абсолютно твердым.
Этой аксиомой пользуются в тех случаях, когда речь идет о равновесии тел, которые нельзя считать твердыми. Приложенные к таким телам внешние силы должны удовлетворять условиям равновесия твердого тела, однако для нетвердых тел эти условия являются лишь необходимыми, но не достаточными.
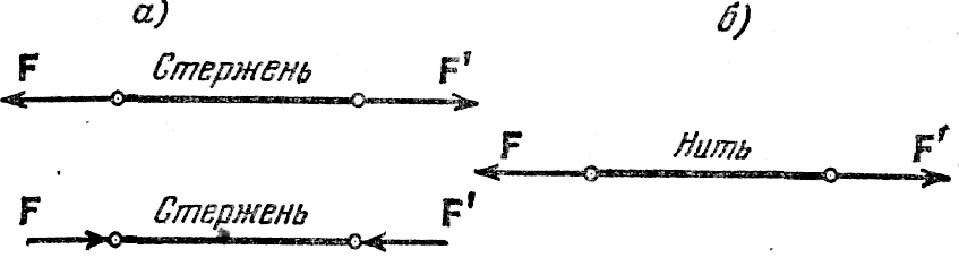
Рисунок 5.
Силы, действующие на нить, были растягивающими (рис. 5), в то время как для стержня они могут быть и сжимающими (рис. а).
Стержень массой 9 кг и длиной 1 м лежит на двух опорах. Одна из них подпирает левый конец стержня, а другая находится на расстоянии 10 см от правого конца. С какой силой действует на стержень каждая из опор?
Решение
Требуется найти силы реакции опоры $N_1$ и $N_2$. Для решения задачи можем применить условие равновесия (правило моментов): $\Sigma $МО = 0.
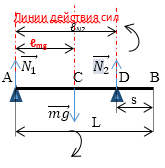
Дано:
$$m = 1 кг$$ $$L = 1 м$$ $$s = 0,1 м$$ $$N_1 - ?$$ $$N_2 - ?$$Определим плечи сил относительно выбранной оси вращения - точки А: $ℓ_{N_1}$ = 0, т.к. линия действия силы проходит через ось вращения; $ℓ_{N_2}$ = AD;
$ℓ_{mg}$ = AC;
$ℓ_{N_2}$ = AD = L - s;
$ℓ_{mg}$ = AC = 0,5L
Определим моменты сил: $МN_2$ = $N_2$•(L - s); $МN_1$ = 0; $Мmg$ = - $mg$•0,5L
Запишем правило моментов $\Sigma $МА = 0: 0 + $N_2$•(L - s) - 0,5mgL = 0, откуда $N_2$•(L - s) = 0,5mgL и $N_2$ = 0,5mgL / (L - s)
$N_2$ = 0,5 • 9 кг • 10 м/с2 • 1 м/ (1 м - 0,1 м) = 50 Н
Аналогично определяем плечи сил и моменты сил относительно точки D: $ℓ_{N_1}$ = AD = L - s; $ℓ_{N_2}$ = 0; $ℓ_{mg}$ = CD = 0,5L - s; $МN_1$ = - $N_1$•(L - s); М$N_2$ = 0.
Правило моментов относительно точки D: $mg$•(0,5L - s) - $N_1$•(L - s) + 0 = 0; Мmg = $mg$•(0,5L - s); $mg$•(0,5L - s) - $N_1$•(L - s) + 0 = 0
$N_1$ = mg•(0,5L - s) / (L - s) = 90 Н•0,4 м / 0,9 м = 40 Н
Ответ: $N_1$ = 40 Н; $N_2$ = 50 Н
Силу $N_1$ можно вычислить двумя способами:
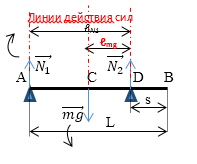
I способ. Так как стержень в равновесии, то условие равновесия справедливо относительно любой оси вращения.
Выберем ось вращения в точке, определим плечи и моменты сил относительно точки D.
После преобразований:
$N_1$ = $mg$•(0,5L - s) / (L - s)
$N_1$ = 40 Н
II способ найти $N_1$.
Т. к. стержень неподвижен, то должно выполняться и другое условие равновесия $\sum{\overrightarrow{F}}$=0
$m\overrightarrow{g}+\ {\overrightarrow{N}}_1+{\overrightarrow{N}}_2=0$
Спроецируем силы на вертикальную ось oY, получим -$mg$ + $N_1$ + $N_2$ = 0
Откуда выразим $N_1$ = $mg$ - $N_2$
$N_1 = 9 кг • 10 м/с2 - 50 Н = 40 Н$
Оба способа дали одинаковый ответ.











