Заполнение атомных состояний электронами. Атомные оболочки и подоболочки

Заполнение атомных состояний электронами

Атом является сложной системой. Электроны взаимодействуют между собой и перемещаются в поле ядра. Однако в атоме можно вводить понятие о состоянии движения каждого отдельного электрона. При этом говорят о стационарных состояниях движения электрона в некотором поле, имеющем центральную симметрию. При этом поле создается ядром и остальными электронами. В общем случае для каждого атома поля отличаются, но определяются одновременно. Такое поле называют самосогласованным.

Так как самосогласованное поле имеет центральную симметрию, то каждое состояние электрона определено величиной орбитального момента. Состояние каждого электрона имеет номер (при заданном орбитальном квантовом числе ($l$) ) -- это главное квантовое число ($n=l+1,\ l+2,\dots $). С увеличением главного квантового числа энергия электрона увеличивается. В атоме водорода энергия не зависит от орбитального квантового числа. В многоэлектронных атомах уровень, например с $n=5,l=0$ расположен ниже по энергии, чем уровень $n=4,l=2$.

В зависимости от значения орбитального квантового числа $l\ $состояние электрона в атоме обозначают разными буквами. Значениям $l=0,1,2,3,4,5\dots $ ставятся в соответствие буквы $s,p,d,f,g,h$ и по алфавиту.

Распределение электронов по состоянию в атоме записывают при помощи спектроскопических символов (Табл.1):

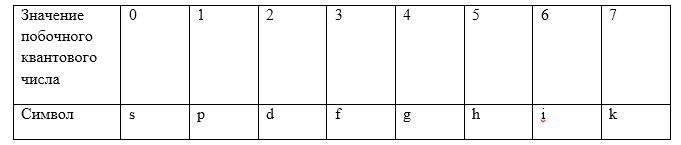
Рисунок 1.

Электронную структуру записывают так: число, находящееся слева -- главное квантовое число ($n$), сам спектроскопический символ соответствует величине орбитального квантового числа ($l$).

Полное описание состояния атома требует вместе с указанием полных $L,S,J$ перечисления всех состояний электронов. Так, например, запись: $1s2p^3P_0$ обозначает состояние атома гелия, имеющего $L=1,S=1,J=0$ и два электрона в состояниях $1s$ и $2p$. В том случае, если несколько электронов находятся в состояниях с одинаковыми $n\ и\ l\ $, то данный факт обозначают как степень. $2p^3$ - три электрона в состоянии $2p$.

О распределении электронов в атоме по состояниям с разными $n\ и\ l$ говорят как об электронной конфигурации.

При известных $n\ и\ l$ электрон может иметь разные значения проекций орбитального момента ($m_l$) и спина ($m_s$) на ось $Z$.

В соответствии с принципом Паули: В атоме не может быть двух электронов, которые бы характеризовались одинаковыми четверками квантовых чисел ($n,l,m_l,\ m_s$), то есть в одном и том же состоянии не может находиться больше, чем один электрон.

Так, если два электрона имеют одинаковые главные квантовые числа ($n$) и орбитальные числа совпадают, то спины их должны быть ориентированы противоположно (то есть их квантовые числа $m_s\ равны\ \frac{1}{2}\ и-\frac{1}{2}$). Данный принцип использовался для обоснования периодической системы Менделеева, части закономерностей в спектрах.

Анализируя строение атома в первом приближении энергией взаимодействия электронов пренебрегают. Считают, что сумма энергия атома равна сумме энергий электронов в поле ядра, которая известна. Значит, не составляет особого труда определить каково распределение электронов по разным состояниям, принимая во внимание принцип Паули. Получается схема заполнения оболочек, которая, надо отметить, все же отличается от реальной, но является полезной.

По поводу взаимного расположения уровней с одинаковой конфигурацией, но разными $L,S$ имеется эмпирическое правило Хунда:

• ниже по энергии расположен терм, мультиплетность которого максимальна;
• если мультиплетности равны, то минимальна энергия у терма, которому принадлежит максимальная величина суммы орбитального момента.

Итак, заполнение электронных состояний определено двумя принципами:

1. принципом Паули.

2. принципом минимума энергии.

Атомные оболочки и подоболочки

Максимальное количество электронов при известном числе n равно $2n^2$. Сумма электронов в много электронном атоме, которые имеют одинаковые главные квантовые числа ($n$) называют электронной оболочкой. В этих оболочках электроны распределены по подоболочкам, которые соответствуют орбитальному квантовому числу ($l$). Так как $l$ изменяется от $0$ до $n-1$, то количество подоболочек равно порядковому номеру подоболочки. Число электронов в подоболочке определяет магнитное и магнитное спиновое квантовые числа. Максимальное количество электронов в подоболочке с известным $l$ равно $2(2l+1)$. Обозначение оболочек и распределение электронов по оболочкам и подоболочкам сведены в табл. 2.

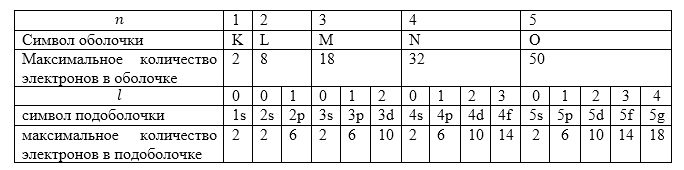
Рисунок 2.