Полосатые и линейчатые спектры
Светящиеся газы показывают линейчатые спектры излучения, которые состоят из отдельных линий. Если свет пропускать через газ, то появляются линейчатые спектры поглощения, при этом атом поглощает спектральные линии, которые сам способен испускать. Первым изучался спектр атома водорода. Во второй половине XIX века проводились множество исследований спектров излучения. Было получено, испускаемый молекулярный спектр представляет собой совокупность широких размытых полос, у которых отсутствуют резкие границы. Такие спектры получили названия полосатых.
Спектр излучения атомов принципиально отличен по виду. Он состоит из четко обозначенных линий. Спектры атомов называют линейчатыми. Для каждого элемента есть определенный испускаемый только им линейчатый спектр. При этом вид спектра излучения не зависит от способа, которым возбужден атом. По такому спектру определяют принадлежность спектра элементу.
Закономерности в линейчатых спектрах
Линии в спектре расположены закономерно. Найти данные закономерности и объяснить их - важная задача физического исследования. Первым эмпирическую формулу, которая описала часть линий излучения для спектра атома водорода, получил Бальмер. Он отметил, что длины волн, девяти линий спектра водорода, которые были известны в то время, могут вычисляться по формуле:
где $\lambda =364,613\ нм,\ n=3,4,\dots ,11.$
Анализ экспериментальных материалов показал, что отдельные линии в спектре можно объединять в группы линий, которые называют сериями. Ридберг записал формулу (1) в виде:
где $R=3,29\cdot {10}^{15}c^{-1}$- константа Ридберга, ${\nu }_{n2}$ -- частота излучения соответствующей линии. Такая серия носит имя Бальмера. Формула Бальмера -- Ридберга (2) указала на специальную роль целых чисел в закономерностях, которые описывают спектры. Данное выражение играло существенную роль в развитии учения о строении атомов.
Сейчас известно много спектральных линий водорода, частоты которых с большой точностью подчинены формуле (2). С ростом $n$ линии в спектре серии приближаются друг к другу. Граница Бальмеровской серии определена с помощью длины волны (${\lambda }_{gran}$), при данной длине волны $n\to \infty :$ ${\lambda }_{gran}=\frac{4}{R}=364,5968$ нм.
Другой ученый, Лайман, исследовал серию линий в ультрафиолетовой части спектра атома водорода и открыл серию, которую описал выражением:
Данную серию называют серией Лаймана.
Серию в инфракрасной области спектра атома водорода описал Пашен:
Такая серия названа в его честь (серия Пашена). Поздние в инфракрасной области спектра атома водорода были найдены следующие серии:
Брэкета:
Пфундта:
Хэмфри:
Каждая из приведенных серий имеет сгущение линий при росте чисел $n$ и свою граничную частоту (длину волны).
Рассматривая приведенные выше формулы, вводя обозначение: $T\left(n\right)=\frac{R}{n^2}$, то каждую испускаемую частоту можно записать как разность (для разных значений целых чисел):
Серию линий спектра получают в соответствии с формулой (8), если одно из целых чисел фиксируется, а другое принимает все целые значения, которые больше числа, которое фиксировано.
Граничные частоты (граничные волновые числа) серий спектра водорода определены как:
Формула (8) подтверждается эмпирически с высокой спектроскопической точностью. Особая роль целых чисел, ставшая очевидной в закономерностях спектров, до конца была осмыслена только в квантовой механике.
Задание: Какова максимальная ($E_{max}$) и минимальная ($E_{min}$) энергии фотона в серии Бальмера?
Решение:
В качестве основы для решения задачи используем сериальную формулу для частот спектра атома водорода:
\[{\nu }_{n2}=R\left(\frac{1}{2^2}-\frac{1}{n^2}\right)\left(n=3,4,5,\dots \right)\left(1.1\right),\]где $R=3,29\cdot {10}^{15}c^{-1}$- константа Ридберга.
Минимальная энергия фотона может быть вычислена при использовании выражения:
\[E=h\nu \ \left(2.2\right)\]при $n=3.$
\[E_{min}=hR\left(\frac{1}{2^2}-\frac{1}{3^2}\right)=\frac{5}{36}hR.\]Максимальная энергия находится при $n=\infty $:
\[E_{max}=hR\left(\frac{1}{2^2}-\frac{1}{{\infty }^2}\right)=\frac{1}{4}hR.\]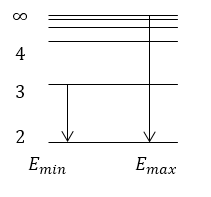
Рисунок 1.
Ответ: $E_{min}=\frac{5}{36}hR,\ E_{max}=\frac{1}{4}hR.$
Задание: Определите, какова длина волна, которая соответствует: 1) границе серии Лаймана, 2) границе серии Бальмера.
Решение:
1) В качестве основы для решения задачи используем сериальную формулу для длин волн спектра водорода (серия Лаймана):
\[\frac{1}{{\lambda }_1}=R'\left(\frac{1}{1^2}-\frac{1}{n^2}\right)\left(n=2,3,4,\dots ,\infty \right)\left(2.1\right),\]где $R'=1,1\cdot {10}^7м^{-1}.$ На границе $n=\infty \ $преобразуем выражение (2.1) в формулу:
\[\frac{1}{{\lambda }_1}=R'\left(\frac{1}{1^2}\right)\to {\lambda }_1=\frac{1}{R'}.\]Проведем вычисление:
\[{\lambda }_1=\frac{1}{1,1\cdot {10}^7}=0,91\cdot {10}^{-7}\left(м\right).\]2) В качестве основы для решения второй части задачи используем сериальную формулу для длин волн спектра водорода (серия Бальмера):
\[\frac{1}{{\lambda }_2}=R'\left(\frac{1}{2^2}-\frac{1}{n^2}\right)\left(n=3,4,\dots ,\infty \right)при\ n=\infty \to \frac{1}{{\lambda }_2}=R'\frac{1}{2^2}\left(2.2\right),\]Получим искомую длину волны:
\[{\lambda }_2=\frac{4}{R'}.\]Проведем вычисления:
\[{\lambda }_2=\frac{4}{1,1\cdot {10}^7}=364\cdot {10}^{-9}\left(м\right).\]Ответ: ${\lambda }_1=910нм$, ${\lambda }_2=364\cdot {10}^{-9}$нм.











