Переходы внутренних электронов в атомах
Если рассматривать электромагнитные переходы валентных (внешних) электронов, то они связаны с излучением волн, длины которых находятся в оптическом диапазоне (это инфракрасная, видимая и ультрафиолетовая области спектра излучения). При переходах, которые связаны с изменением состояния внутренних электронов, возникает линейчатое рентгеновское излучение. Энергия квантов рентгеновского излучения может достигать значений порядка ${10}^5эВ$.
Самым существенным отличием рентгеновских от оптических спектров является то, что рентгеновские спектры разных элементов схожи друг с другом, тогда как оптические спектры являются индивидуальными. Данный факт объясняют тем, что изменение числа электронов на внешней оболочке ведет к радикальным изменениям в спектре энергии. Внутренние электроны атомов находятся в потенциальном поле ядра, которое частично экранируется оболочкой электронов. Как следствие, энергия внутренних электронов изменяется плавно при изменении заряда ядра, при этом качественного структурного изменения спектра не происходит.
Электроны внутренних оболочек атомов, прежде всего, взаимодействуют с ядром атома, и только в следующую очередь между собой. Потенциал ядра можно считать кулоновским, а взаимодействие электронов при необходимости учитывают, применяя теорию возмущений. Это означает то, что внутренние электроны атома могут быть описаны в одночастичном приближении. При этом их волновые функции и положения энергоуровней можно считать водородоподобными. Довольно часто при описании спектра энергий внутренних электронов в атоме используют приближение так называемого эффективного заряда:
где $n$ -- главное квантовое число, $l$ --орбитальное квантовое число, ${\sigma }_{nl}$ -- постоянная экранирования. Так, для электрона легкого элемента, который расположен на K- оболочке ${\sigma }_{1l}\approx 1$. Это значит, что поле ядра частично экранировано другим электроном, который локализован на той же оболочке. Если переходить к оболочкам, которым соответствует большее значение главного квантового числа, то есть оболочкам $L,M$,..., величина коэффициента ${\sigma }_{nl}$ будет увеличиваться. Коэффициент экранирования растет в связи с увеличением количества внутренних электронов. Рост его сильнее при увеличении квантового числа $l$ для рассматриваемого электрона.
Если удалить один из электронов атома, локализованный на K- оболочке атома со многими электронами. В таком случае становятся возможны переходы электронов на $K$ -- оболочку с оболочек более высоких ($L,M$,....). При этом появляется $K$- серия рентгеновского излучения (рис.1). Номера линий в серии обозначаются при помощи букв греческого алфавита. Так, переход с оболочки $L$ на $K$- оболочку образует линию $K_{\alpha }$ рентгеновского излучения, при переходе с $M$ -- оболочки на $K$- оболочку возникает $K_{\beta }$ линия и т.д. При создании вакантного места на атомной $L$ - оболочке переходы с атомных оболочек, которые расположены выше, создают $L$ -- серию рентгеновского излучения. Следом возникает $M$ - серия линейчатого рентгеновского излучения.
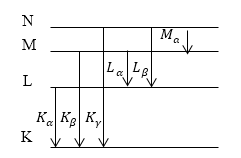
Рисунок 1.
Если использовать выражение (1) для энергии внутреннего электрона, находящегося в атоме, можно получить формулу для расчёта частот квантов характеристического излучения для элемента, который имеет заряд ядра равный $Z$:
где ${\sigma }_1\ $- постоянная экранирования для нижнего состояния, ${\sigma }_2\ $- постоянная экранирования для верхнего состояния между которыми происходит переход с испусканием рентгеновского кванта. Разница между ${\sigma }_1\ $и ${\sigma }_2$ очень мала, поэтому чаще всего используют эффективную постоянную $\sigma $ для того и другого состояния. В таком случае выражение (2) преобразуется к виду:
Выражение в виде (3) для возможных величин частот линейчатого рентгеновского излучения практически совпадает с обобщенной формулой Бальмера, которая определяет закономерности спектра в атоме водородоподобных ионов.
Рассмотрим выражение (3). Если $n_1=1,$ $n_2\ge 2$, то мы имеем дело с $K$ - серией рентгеновского излучения. При $n_1=2,$ $n_2\ge 3$ получим $L$ - серии, при $n_1=3,$ $n_2\ge 4$ - $M$ -- серии. Кроме того из выражения (3) получим, что энергия рентгеновского кванта $K_{\alpha }$ -- линии равна:
где $R$ -- постоянная Ридберга. Из формулы (4) видно, что выражение для энергии рентгеновского кванта $K_{\alpha }$ -- линии совпадает с энергией кванта головной линии серии Лаймана в ионе водорода (водородоподобном ионе) с точностью до постоянной экранирования. Для $L_{\alpha }$ -- линии характеристического излучения выполняется равенство:
где постоянная экранирования ${\sigma }_L\ $определяется из эксперимента или расчетов электронной структуры атома. При этом получают, что $2
Примеры задач
Каким будет порядковый номер элемента в периодической системе, если частота границы $K$ - серии линейчатого рентгеновского излучения равна ${\nu }_{\infty }Гц$? Считайте элемент легким.
Решение:
В качестве основы для решения задачи используем формулу для возможных величин частот линейчатого рентгеновского излучения вида:
\[\nu =R{\left(Z-\sigma \right)}^2\left(\frac{1}{n^2_1}-\frac{1}{n^2_2}\right)\left(1.1\right),\]где для $K$- серии $n_1=1$. $n_2$ положим равным бесконечности, так как нам задана граничная частота $K$ - серии. Так как по условию задачи рассматриваемый элемент считается легким, то постоянную экранирования можно считать равной единице ($\sigma =1$). Используя выше сказанное, запишем выражение (1.1) как:
\[{\nu }_{\infty }=R{\left(Z-1\right)}^2\left(\frac{1}{n^2_1}\right)=R{\left(Z-1\right)}^2\left(1.2\right).\]Из формулы (1.2) выразим искомый порядковый номер элемента:
\[Z=\sqrt{\frac{{\nu }_{\infty }}{R}}+1.\]Ответ: $Z=\sqrt{\frac{{\nu }_{\infty }}{R}}+1.$
Какой будет постоянная экранирования для $L$ -- серии характеристического рентгеновского излучения в том случае, если при переходе электрона в атоме с оболочки $M$ на оболочку $L$ длина волны фотона, который испускается, равна $\lambda $, номер атома в периодической системе $Z$?
Решение:
При переходе электрона с $M$ --оболочки на $L$ -- оболочку возникает $L_{\alpha }$ линия спектра. При этом в выражении:
\[\nu =\frac{1}{\lambda }=\frac{5}{36}R{\left(Z-{\sigma }_L\right)}^2\left(2.1\right).\]Из формулы (2.1) выразим искомую величину -- постоянную экранирования, получим:
\[{\sigma }_L=Z-\sqrt{\frac{36}{5R\lambda }}.\]Ответ: ${\sigma }_L=Z-\sqrt{\frac{36}{5R\lambda }}.$











