При рассмотрении нерелятивистского электрического взаимодействия микрочастиц спин не учитывают. С точки зрения математики это значит, что гамильтониан системы заряженных частиц при отсутствии магнитного поля не имеет операторов спина, значит, применение его к волновой функции не действует на спиновые переменные. Волновая функция при этом может быть представлена как произведение:
где $\varphi \left({\overrightarrow{r}}_1,{\overrightarrow{r}}_2,\dots \right)=R_{n,l}Y_{l,m}-\ $зависит только от координат частиц (пространственная (координатная или орбитальная) волновая функция), $\gamma \left({\alpha }_1,{\alpha }_2,\dots ,\right)$ - зависит от спинов частиц (спиновая волновая функция). Уравнение Шредингера определяет орбитальную функцию ($\varphi $). Если спин частиц для решения поставленных задач, существенным не является, применяют уравнение Шредингера и функцию $\varphi .$ Но, следует отметить, что если электрическое взаимодействие частиц не зависит от спина, то энергия системы от полного спина зависит. Что является следствием тождественности частиц.
Рассмотрим систему из двух одинаковых частиц. Решая уравнение Шредингера, мы получим совокупность уровней энергии. Каждому такому уровню энергии соответствует пространственная волновая функция, которая является симметричной или антисимметричной ($\varphi ({\overrightarrow{r}}_1,{\overrightarrow{r}}_2)$).
Пусть частицы имеют спин равный нулю. Спиновый множитель в данном случае отсутствует. Координатная функция должна быть симметричной (имеем дело с бозе частицами). Не все уровни энергии при формальном решении уравнения Шредингера реализуются. Рассматриваются только те, которые соответствуют симметричным функциям $\varphi .$ Система из двух частиц с нулевым спином имеет только четный орбитальный момент.
Рассмотрим систему из двух электронов. Их спины равны $\frac{1}{2}.$ В данном случае $\psi \left(q_1,q_2\right)$ является антисимметричной. Это означает, что при симметричной координатной функции спиновая волновая функция будет антисимметричной (и наоборот). Чаще всего спиновую функцию в квантовой механике записывают в виде спинора (например, как спинор второго ранга ${\gamma }^{\alpha \beta },\ $где индексы обозначают спин одного из электронов). Антисимметричный спинор:
Симметричный спинор второго ранга описывает систему с полным спином равным единице (триплетное состояние), а антисимметричный спинор сведется к скаляру, при этом спин равен нулю (синглетное состояние). Это означает, что значения энергии, которые связаны с антисимметричными функциями $\varphi ,$ требуют полного спина, который равен единице (спины электронов «параллельны»). То есть возможные варианты значений энергии системы электронов зависят от полного спина. При этом говорят о специфическом взаимодействии частиц, которое ведет к такой зависимости. Данный вид взаимодействия называют обменным. Это исключительно квантовый вид взаимодействия. При переходе к классической механике этот эффект полностью исчезает (как и само понятие спина).
Не следует считать обменную энергию особым видом энергии. Она является результатом принципиальной неразличимости двух квантовых состояний, одно из которых получено как перестановка одинаковых взаимодействующих частиц.
Обменное взаимодействие возможно не только для сил Кулона, но и для любых других сил, которые возможны в системе одинаковых частиц, не зависимо от их природы. Так, обменное взаимодействие имеет место между нуклонами ядра атома. Оно проявляется в насыщении ядерных сил. Ферромагнетизм был объяснен с применением понятия обменного взаимодействия.
Простейшей системой, в которой рассматривают обменное взаимодействие, является двухэлектронный атом гелия (или молекула водорода). При этом рассматривают возбужденные уровни гелия. Обменное взаимодействие ведет к расщеплению энергоуровней. Возбужденные уровни в парагелии являются синглетами, а в ортогелии триплетами. Орто и парагелий один химический элемент, но находящийся в разных квантовых состояниях.
Для $1snl$ конфигурации расчет энергии взаимодействия электронов проводят как:
где:
- \[I_k=\int{{\left|{\varphi }_{1s}\left({\overrightarrow{r}}_1\right)\right|}^2}{\left|{\varphi }_{nl}\left({\overrightarrow{r}}_2\right)\right|}^2\frac{{q_e}^2}{\left|{\overrightarrow{r}}_1-{\overrightarrow{r}}_2\right|}dV_1dV_2(4)\] - энергия взаимодействия двух «размазанных» электронов (с силами Кулона),
- \[I_{ob}=\int{{\varphi }_{1s}\left({\overrightarrow{r}}_1\right)}{\varphi }_{nl}\left({\overrightarrow{r}}_2\right){{\varphi }_{1s}}^*\left({\overrightarrow{r}}_2\right){{\varphi }_{nl}}^*\left({\overrightarrow{r}}_1\right)\frac{{q_e}^2}{\left|{\overrightarrow{r}}_1-{\overrightarrow{r}}_2\right|}dV_1dV_2(5)\] - обменная энергия. Данная энергия не имеет классического толкования. Она является частью (в данном случае) энергии взаимодействия двух электронов. Образно говоря, $I_{ob}$ возникает так как любой электрон находится в состоянии ${\varphi }_{1s}\ и\ {\varphi }_{nl}.\ $При этом знак плюс в выражении (3) соответствует синглетному состоянию терма, знак минус -- триплету. Из формулы (3) становится очевидным, что величина энергии триплетного состояния меньше, чем синглетного. С точки зрения физики это понятно. Если пространственная функция является симметричной ($S=0$, спины являются антипараллельными), то электроны располагаются ближе друг к другу, значит энергия их взаимодействия выше, чем у триплета. В триплетном состоянии пространственная волновая функция антисимметрична, электроны более удалены друг относительно друга.
Так, взаимодействие электронов ведет к тому, что термы, обладающие одной конфигурацией, имеют разную энергию, при этом ниже по энергии находится триплет. Схему расщепления можно изобразить как на рис.1
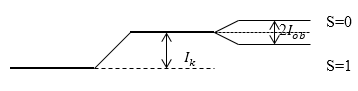
Рисунок 1.
Задание: Возбужденное состояние атома имеющего электронную конфигурацию $nsn^l$, где $n\ne n'$ соответствуют два терма вида: ${}^1L$ и ${}^3L$, где $L$ -- суммарный орбитальный момент, $L=l$. Покажите, что если рассмотреть взаимодействие между электронами как возмущение можно показать, что энергия триплета ниже, чем энергия синглета.
Решение:
Пространственную компоненту волновой функции для стационарных состояний атома можно представить как:
\[\varphi =\frac{1}{\sqrt{2}}\left\{{\varphi }_1\left({\overrightarrow{r}}_1\right){\varphi }_2\left({\overrightarrow{r}}_2\right)\pm {\varphi }_2\left({\overrightarrow{r}}_1\right){\varphi }_1\left({\overrightarrow{r}}_2\right)\right\}\left(1.1\right),\]где плюс относится к синглету, минус к триплету. При этом ${\varphi }_1\left(\overrightarrow{r}\right)$ представляет волновую функцию $ns-$электронов, а ${\varphi }_2\left(\overrightarrow{r}\right)$ описывает состояние $n'l$ -- электронов. При этом мы понимаем, что рассматриваем только электроны, которые находятся вне заполненных оболочек. Присутствие электронов заполненных оболочек проявляется в записи конкретного вида волновых функций (${\varphi }_{12}$), который определяется самосогласованным полем. Если взаимодействие $ns-и\ n'l$ -- электронов не учитывать в волновой функции (1.1), то изменение энергии за счет взаимодействия можно определить как:
\[\triangle E_{s\left(a\right)}=I_k\pm I_{ob}\ \left(1.2\right),\]где обменный интеграл равен:
\[I_{ob}=\int{{\varphi }_1\left({\overrightarrow{r}}_1\right)}{\varphi }_2\left({\overrightarrow{r}}_2\right){{\varphi }_1}^*\left({\overrightarrow{r}}_2\right){{\varphi }_2}^*\left({\overrightarrow{r}}_1\right)\frac{{q_e}^2}{\left|{\overrightarrow{r}}_1-{\overrightarrow{r}}_2\right|}dV_1dV_2(1.3)\]и он определяет энергетическое расцепление синглетного и триплетного термов. Сравним, данный интеграл с нулем. Для этого будем считать, что волновая функция ${\varphi }_1$ является вещественной, при этом ${\varphi }_2$ представим как:
\[{\varphi }_2={\xi }_1+i{\xi }_2\left(1.4\right),\]где ${\xi }_1и\ {\xi }_2$ вещественные функции, тогда выражение (1.3) можно преобразовать к виду:
\[I_{ob}=\int{{\frac{{q_e}^2}{\left|{\overrightarrow{r}}_1-{\overrightarrow{r}}_2\right|}\varphi }_1\left({\overrightarrow{r}}_1\right)}{\varphi }_2\left({\overrightarrow{r}}_2\right)\left\{{\xi }_1\left({\overrightarrow{r}}_1\right){\xi }_1\left({\overrightarrow{r}}_2\right)+{\xi }_2\left({\overrightarrow{r}}_1\right){\xi }_2\left({\overrightarrow{r}}_2\right)\right\}dV_1dV_2\left(1.5\right).\]То, что выражение (1.5) является положительным, следует из формулы для энергии электростатического поля, которое создается зарядом, который распределен с плотностью $\rho \left(\overrightarrow{r}\right):$
\[E=\frac{1}{2}\int{\varphi \left(\overrightarrow{r}\right)\rho \left(\overrightarrow{r}\right)dV=}\frac{1}{2}\int{\frac{1}{\left|\overrightarrow{r}-\overrightarrow{r}'\right|}\rho \left(\overrightarrow{r}\right)\rho \left(\overrightarrow{r}'\right)dVdV'>0.}\]Ответ: Так, как $I_{ob} >0$, следует, что энергия триплета ниже, чем энергия синглета.
Задание: Чем объясняется понижение энергоуровней парасостояния гелия и повышение уровней ортосостояния гелия.
Решение:
Понижение энергоуровней парасостояния гелия и повышение уровней ортосостояния гелия объясняется наличием обменной энергии.











