Фактор Ланде
Фактором (множителем) Ланде называют параметр, который определяет масштаб расщепления энергетических уровней при наличии внешнего магнитного поля (в относительных единицах). Предложен А. Ланде в 1921 г, когда он занимался исследованием спектра испускания атомов, которые находятся в магнитном поле.
Рассмотрим легкий атом ($LS$ -связь). Для нахождения полного магнитного момента атома можно воспользоваться схемой сложения моментов (рис.1). На данном рисунке представлено сложение орбитального и спинового механического момента и магнитного моментов атома.
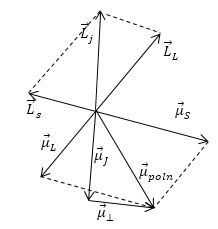
Рисунок 1.
В соответствии с рис.1, имеем:
Из приведенного рис.1, можно записать:
где ${\overrightarrow{L}}_L$ -- полный орбитальный момент. Возведем равенства (2) и (3) в квадраты, получим для косинусов углов между векторами выражения вида:
где для нахождения $L^2_J,\ L^2_L,\ L^2_S\ $применены формулы:
Учтем, что:
где ${\mu }_b=\frac{q_e\hbar }{2m_e}$-- магнетон Бора (система СИ), здесь $m_e$ -- масса электрона. В таком случае представим ${\mu }_J\$ (1), используя выражения (4) и (5) как:
где параметр $g_J$ называют фактором (множителем) Ланде.
где $\left(\overrightarrow{S}\overrightarrow{J}\right)=\frac{1}{2}\left({\overrightarrow{J}}^2+{\overrightarrow{S}}^2-{\overrightarrow{L}}^2\right).$ Тогда $g_J$ или просто $g$,будет равно:
$g=1+\frac{{\overrightarrow{J}}^2+{\overrightarrow{S}}^2-{\overrightarrow{L}}^2}{2{\overrightarrow{J}}^2}\left(13\right).$Из формулы (11) видно, что $g_J$ является гиромагнитным отношением для полного магнитного и механического момента атома.
В том случае, если мы имеем синглет: $Ѕ=0, J=L$ из формулы $12$ следует:
что соответствует гиромагнитному отношению орбитального момента при орбитальном перемещении электрона в атоме.
Если мы имеем $S$ - терм, то есть $L=0, J=Ѕ$ из выражения (12) получаем, что:
что соответствует гиромагнитному отношению спина.
Вообще говоря, фактор Ланде представлен рациональной дробью.
Проекцию магнитного момента атома (${\mu }_{J,Z}$) на направление внешнего магнитного поля (совпадающего с осью $Z$) можно представить как:
где $m_J$ является полным магнитным квантовым числом.
Фактор Ланде входит в магнитомеханическое (гиромагнитное) отношение -- соотношение между дипольным магнитным моментом элементарной частицы (или системы) и ее механическим моментом. Множитель Ланде есть число, которое определяется углом между векторами магнитного момента и механического момента системы электронов атома. Для состояний атома данное соотношение в СИ можно записать как:
где ${\gamma }_0=-\frac{q_e}{2m_e}.$
Фактор Ланде может иметь разные значения. Он может быть и меньше нуля и больше двух.
Частота Лармора ($\hbar \omega $) -- частота прецессии спинового магнитного момента во внешнем магнитном поле ($B$) описывается при помощи фактора Ланде:
В общем случае, спиновое расщепление связано не только с величиной, но и ориентацией магнитного поля. В таком случае фактор Ланде будет тензором:
где $\hbar {\omega }_{\alpha }$- компоненты ларморовской частоты, и $B_{\beta }$ -- составляющие векторов магнитного поля.
Примеры задач
Рассмотрите, каков фактор Ланде для следующих состояний: ${}^3{P_0},{}^6{F_{\frac{1}{2}}}$?
Решение:
-
Рассмотрим терм ${}^3{P_0}$. Для него имеем: $L=1, J=0$, $S=1.$ Вычислим фактор Ланде: \end{enumerate}
$g_J=1+\frac{0}{0}\left(1.1\right)$для состояния ${}^3{P_0}$ получим неопределенность.
такая неопределенность оправдана, так как при $J=0$ механический момент равен нулю, следовательно, равен нулю магнитный момент;
-
Для состояния ${}^6{F_{\frac{1}{2}}}$ множитель Ланде равен:
\[g_{J2}=-\frac{2}{3}\left(1.3\right),\]значит «векторы» механического и магнитного моментов сонаправлены.
Ответ: $g_{J1}=1+\frac{0}{0},\ g_{J2}=-\frac{2}{3}.$
Какова мультиплетность состояния атома ($\tau $), если максимальная величина проекции магнитного момента атома в состоянии $D_2$ равна ${4\ \mu }_b$,
Решение:
В качестве основы для решения задачи применим формулу:
\[{\mu }_{J,Z}={-g}_J{\mu }_Bm_J\left(2.1\right).\]Из условия задачи:
\[{\mu }_{Zmax}=g_JJ{\mu }_B=4{\mu }_B(2.2)\]найдем:
\[g_J=2.\]Мы знаем, что по условию задачи $L=2$ и $J=2$, используем формулу для вычисления фактора Ланде, выразим квантовое число $Ѕ$:
\[S^2+S-12=0\ \to S=3.\]Найдем мультиплетность:
\[\tau =2S+1=7.\]Ответ: $\tau =7.$
Каким будет магнитный момент атома, который находится в состоянии $S=1,\ L=2,\ g=\frac{4}{3}?$
Решение:
В качестве основы для решения задачи используем формулу:
\[{\mu }_J={\mu }_bg\sqrt{J\left(J+1\right)}\left(3.3\right).\]Исходя из условий задачи, найдем квантовое число J:
\[J=S+L\left(3.2\right).\]Подставим имеющиеся значения, найдем искомую величину:
\[{\mu }_J={\mu }_b\frac{4}{3}\sqrt{3\left(3+1\right)}=\frac{8}{3}\sqrt{3}{\mu }_b.\]Ответ: ${\mu }_J=\frac{8}{3}\sqrt{3}{\mu }_b.$











