Опыты Штерна и Герлаха
В $1921$ г. О. Штерн выдвинул идею опыта измерения магнитного момента атома. Данный эксперимент он выполнил в соавторстве с В. Герлахом в $1922$ г. Метод Штерна и Герлаха использует то, что пучок атомов (молекул) способен отклоняться в неоднородном магнитном поле. Атом, который имеет магнитный момент можно представить как элементарный магнит, имеющий малые, но конечные размеры. Если подобный магнит разместить в однородном магнитном поле, то он не испытывает силы. Поле будет действовать на северный и южный полюса такого магнита с силами, которые равны по модулю и противоположны по направлению. В результате, центр инерции атома будет покоиться или двигаться по прямой. (При этом ось магнита может совершать колебания или прецессировать). То есть, в однородном магнитном поле не возникает сил, которые действуют на атом и сообщают ему ускорение. Однородное магнитное поле не изменяет угол между направлениями индукции магнитного поля и магнитного момента атома.
Ситуация складывается иначе, если внешнее поле является неоднородным. В таком случае силы, которые действуют на северный и южный полюса магнита не равны. Результирующая сила, действующая на магнит отлична от нуля, и она сообщает атому ускорение, по полю или против него. Как результат, при перемещении в неоднородном поле рассматриваемый нами магнит отклонится от первоначального направления движения. При этом размер отклонения зависит от степени неоднородности поля. Для того, чтобы получить существенные отклонения поле должно резко изменяться уже в пределах длины магнита (линейные размеры атома $\approx {10}^{-8}см$). Такой неоднородности экспериментаторы добились с помощью конструкции магнита, который создавал поле. Один магнит в опыте имел вид лезвия, другой был плоским или обладал выемкой. Магнитные линии сгущались у «лезвия», так что напряженность в этой области была существенно больше, чем у плоского полюса. Тонкий пучок атомов пролетал между данными магнитами. Отдельные атомы отклонялись в созданном поле. Следы отдельных частиц наблюдались на экране.
Согласно представлениям классической физики в атомном пучке магнитные моменты имеют различные направления по отношению к некоторой оси $Z$. Что означает: проекция магнитного момента ($p_{mz}$) на данную ось принимает все значения интервала от $\left|p_m\right|$ до -$\left|p_m\right|$ (где $\left|p_{mz}\right|-$ модуль магнитного момента). На экране пучок должен получиться расширившимся. Однако, в квантовой физике, если учесть квантование, то возможными становятся не все ориентации магнитного момента, а только конечное их количество. Так, на экране след пучка атомов получался расщепленным на некоторое число отдельных следов.
Поставленные эксперименты показали, что например, пучок атомов лития расщепился на $24$ пучка. Это является обоснованным, так как основной термом $Li - 2S$ -- терм (один валентный электрон, имеющий спин $\frac{1}{2}\ $ на s --орбите, $l=0).$ По размерам расщепления можно сделать вывод о величине магнитного момента. Так Герлах получил доказательство того, что спиновый магнитный момент равен магнетону Бора. Исследования разных элементов показали полное согласование с теорией.
Штерн и Раби измерили магнитные моменты ядер, применяя данный подход.
Итак, если проекция $p_{mz}$ квантована, вместе с ней квантована средняя сила, которая действует на атом со стороны магнитного поля. Опыты Штерна и Герлаха доказали квантование проекции магнитного квантового числа на ось $Z$. Получилось, что магнитные моменты атомов направлены параллельно оси $Z$, под углом к данной оси они направлены быть не могут, так пришлось принять то, что ориентация магнитных моментов относительно магнитного поля изменяется дискретно. Данное явление было названо пространственным квантованием. Дискретность не только состояния атомов, но и ориентировок магнитных моментов атома во внешнем поле -- принципиально новое свойство перемещения атомов.
Полностью опыты были объяснены после открытия спина электрона, когда получили то, что магнитный момент атома вызван не орбитальным моментом электрона, а внутренним магнитным моментом частицы, который связан с его внутренним механическим моментом (спином).
Расчет движения магнитного момента в неоднородном поле
Пусть атом движется в неоднородном магнитном поле, его магнитный момент равен ${\overrightarrow{p}}_m$. На него действует сила:
Вцелом, атом является электрически нейтральной частицей, поэтому другие силы на него в магнитном поле не действуют. Исследуя движение атома в неоднородном поле можно измерить его магнитный момент. Допустим, что атом перемещается по оси $X$, неоднородность поля создана в направлении оси $Z$ (рис.1):
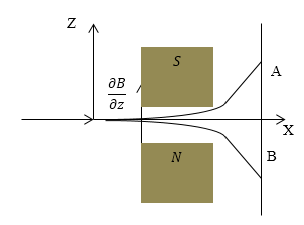
Рисунок 1.
\frac{}{}\frac{}{}
Используя условия (2) выражение (1) преобразуем к виду:
Магнитное поле симметрично относительно плоскости y=0. Можно предположить, что атом перемещается в данной плоскости, значит $B_x=0.$ Равенство $B_y=0$ нарушается только в небольших областях у краев магнита (этим нарушением пренебрегаем). Из выше сказанного следует, что:
В таком случае выражения (3) имеют вид:
Прецессия атомов в магнитном поле не влияет на $p_{mz}$. Уравнение движения атома в пространстве между магнитами запишем в виде:
где $m$ -- масса атома. Если атом проходит путь $a$ между магнитами, то он отклоняется от оси X на расстояние, равное:
где $v$ -- скорость атома по оси $X$. Уходя из пространства между магнитами атом продолжает перемещаться под неизменным по отношению к оси $X$ углом по прямой. В формуле (7) величины $\frac{\partial B_z}{\partial z}$, $a$, $v\ и\ m$ известны, измерив z можно сосчитать $p_{mz}$.
Задание: На сколько компонент, при проведении опыта аналогичного опыту Штерна и Герлаха, произойдёт расщепление пучка атомов, если они находятся в состоянии ${}^3{D_1}$?
Решение:
Терм расщепляется на $N=2J+1$ подуровней, если множитель Ланде $g\ne 0$, где
\[g=1+\frac{J\left(J+1\right)+S\left(S+1\right)-l\left(l+1\right)}{2J\left(J+1\right)}\left(1.1\right).\]Для нахождения числа компонент, на которое расщепится пучок атомов, нам следует определить полное внутреннее квантовое число $(J)$, мультиплетность $(S)$, орбитальное квантовое число, сравнить множитель Ланде с нулем и если он отличен от нуля, то вычислить число подуровней.
1) Для этого рассмотрим структуру символической записи состояния атома ($3D_1$). Наш терм расшифруется следующим образом: символу $D$ соответствует орбитальное квантовое число $l=2$, $J=1$, мультиплетность $(S)$ равна $2S+1=3\to S=1$.
Вычислим $g,$ применив формулу (1.1):
\[g=1+\frac{1\left(1+1\right)+1\left(1+1\right)-2\left(2+1\right)}{2\left(1+1\right)}=-1\ne 0.\]Количество компонент, на которые расщепится пучок атомов, равен:
\[N=2J+1(1.1)\]То есть:
\[N=2+1=3.\]Ответ: $N=3.$
Задание: Почему в опыте Штерна и Герлаха по обнаружению спина электрона применяли пучок атомов водорода, которые находились в $1s$ состоянии?
Решение:
В $s-$ состоянии момент импульса электрона $(L)$ равен нулю, так как $l=0$:
\[L=\hbar \sqrt{l\left(l+1\right)}(2.1)\]Магнитный момент атома, который связан с движением электрона по орбите, пропорционален механическому моменту:
\[{\overrightarrow{p}}_m=-\frac{q_e}{2m}\overrightarrow{L}(2.2)\]следовательно, равен нулю. Это означает, что магнитное поле не должно влиять на перемещение атомов водорода в основном состоянии, то есть расщеплять поток частиц. Но при использовании спектральных приборов было показано, что линии спектра водорода проявляют наличие тонкую структуру (дублеты) даже если магнитного поля нет. Для того, чтобы объяснить наличие тонко структуры и была выдвинута идея собственного механического момента импульса электрона в пространстве (спина).












