Электрический ток может существовать не только в проводах. К примеру, почва является хорошим проводником. Возникает проблема расчета сопротивления подобной среды, даже если известна ее удельная проводимость.
Формула, для расчета сопротивления однородной проводящей сплошной среды
Рассмотрим однородную сплошную среду, погрузим в нее электроды. Между электродами протекает эклектический ток. Линии плотности тока ($\overrightarrow{j}$) совпадают с линиями напряженности ($\overrightarrow{E}$) поля в среде и выполняется равенство:
При этом сила тока через замкнутую поверхность S, которая окружает один из электродов, равна:
Представим, что проводящую среду удалили. Рассмотрим электроды как обкладки конденсатора. В таком случае его емкость (С) можно представить как:
где $q$ -- заряд на электроде, $U$ -- разность потенциалов между электродами. По теореме Остроградского -- Гаусса получим:
где $\overrightarrow{E}$ -- напряженность поля конденсатора, S та же самая поверхность, что и в (2). Вследствие единственности решения задач электростатики разность потенциалов между электродами однозначно определяет напряжённость поля. Значит, напряженность поля в уравнении (2) (в среде в которой течет ток), совпадает с напряженностью поля, которое создают эти же электроды в вакууме при той же разности потенциалов (4). Следовательно, делаем вывод о том, что:
В таком случае сопротивление однородной среды зададим с помощью формулы:
Условия применимости формулы расчета сопротивления для сплошной среды
Все, что сказано выше не применяется для неоднородной среды, так как в ней при прохождении тока возникают объемные заряды, которые в свою очередь являются источниками поля. Поле в среде при прохождении тока не совпадает с полем в вакууме.
Формула (6) позволяет вычислить электросопротивление сплошной среды, если известна емкость конденсатора, обкладками которого в данном случае служат электроды. Результаты вычислений выше, чем лучше соблюдается постоянство потенциалов электродов. В том случае, когда разные точки электродов имеют разный потенциал при прохождении тока, расчет сопротивления не сводится к вычислению емкости конденсатора. В частности, необходимо, чтобы удельное сопротивление электродов должно быть существенно меньше, чем удельное сопротивление среды или размеры электродов могут быть малы.
Заземление
Рассмотрим задачу о сопротивлении заземления в общем виде. На рис.1 изображены две станции (1 и 2). Связь между ними осуществляется с помощью провода 12. Другим проводом служит земля. Около каждого из заземленных тел, которые в данном случае играют роль электродов А и В будем считать среду однородной с удельными проводимостями ${\sigma }_1$ и ${\sigma }_2$.

Рис. 1
Считаем, что электроды находятся глубоко в земле, следовательно, влияние границы на общий ток, который течет между электродами, не существенно. Допустим, что емкости электродов в вакууме $C_1$ и $C_2$. Ток стекающий с положительного электрода А, зависит от его потенциала ${\varphi }_1$ и электропроводимости почвы около электрода. Этот ток почти не зависит от свойств удаленных областей окружающей среды (будем считать, что ${\sigma }_1=const$). Положим $\varphi \left(\infty \right)=0$, используем формулу для вычисления сопротивления сплошной среды (6) следовательно:
Так как станции соединены проводом 12, следовательно: $I_1=I_2=I$, тогда найдем разность потенциалов:
Следовательно, сопротивление заземления равно:
Нельзя полагать, что весь ток с электрода A попадет на электрод В, это не верно. Равны только токи $I_1=I_2$, так как электроды соединены проводом. Формула (9) означает, что для хорошего заземления электроды должны иметь большой размер. Окружающая их почва должна иметь хорошую проводимость.
Задание: Произошел обрыв высоковольтной линии электропередач. Конец линии длинной L=30м лежит на земле. В прилегающих к проводу участках земли идет ток (I=500A). Рассчитайте напряжение шага человека ($U_{sh}$), который идет около провода в перпендикулярном к нему направлении. Расстояние его ближайшей к проводу ноги равно d=1м, длина шага l=0,65м.
Решение:
Так как провод с током имеет большую длину, считаем, что ток от него вглубь земли течет по направлениям перпендикулярным проводу. Ток растекается равномерно в полуцилиндрическую область. В таком случае выражение для плотности тока (j) на расстоянии r от провода имеет вид:
\[j=\frac{I}{\pi rL}\left(1.1\right).\]В таком случае напряженность поля вдоль радиусов, перпендикулярных проводу:
\[E_r=\frac{j}{\sigma }=\frac{I}{\pi rL\sigma }\left(1.2\right).\]В таком случае, напряжение шага можно найти как:
\[U_{sh}=\int\limits^{d+l}_d{E_rdr}=\frac{I}{\pi L\sigma }ln\frac{d+l}{d}\left(1.3\right).\]Проведем вычисления, так как все величины в (1.3) известны, единицы их представлены в системе СИ:
\[U_{sh=}\frac{500}{3,14\cdot 30\cdot {10}^{-2}}ln\frac{1+0,65}{1}=265\ \left(В\right).\] \[\ для\ влажной\ земли\ \sigma =\frac{См}{м}.\]Ответ: $U_{sh=}265\ В.$
Задание: Между двумя коаксиальными цилиндрическими электродами радиусами${\ R}_1$ и $R_2$ находится сплошная проводящая среда с удельной проводимостью $\sigma $. Вычислите сопротивление этой среды. Считать, что удельная проводимость материала жилы и оболочки много больше, чем удельная проводимость среды. Высота цилиндров равна l.
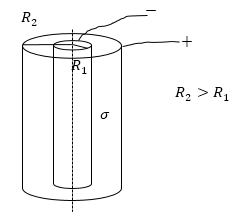
Рис. 2
Решение:
Ток в среде течет во всем объеме по радиусам от центральной жилы до оболочки. Емкость цилиндрического конденсатора нам известна:
\[C=\frac{2\pi l{\varepsilon }_0}{ln\frac{R_2}{R_1}}\left(2.1\right).\]В таком случае сопротивление среды равно:
\[R=\frac{{\varepsilon }_0}{\sigma C}=\frac{ln\frac{R_2}{R_1}}{2\pi \sigma l}\left(2.2\right).\]Ответ: $R=\frac{ln\frac{R_2}{R_1}}{2\pi \sigma l}$.











