Интегральная формулировка закона Би-Савара-Лапласа
Уравнение, описывающее возникновение магнитного поля электрическим током, называется законом Био-Савара-Лапласа. Био и Савар установили его экспериментально, Лаплас облек в его математическую форму. Для замкнутого тока данный закон записывается как:
где $\overrightarrow{r}$ -- радиус-вектор, проведенный от элемента тока $Id\overrightarrow{l}$ к точке, в которой ищется индукция магнитного поля ($\overrightarrow{B}$), ${\mu }_0=4\pi \cdot {10}^{-7}\frac{Гн}{м}(в\ СИ)$ - магнитная постоянная. Интегрирование проводят по замкнутому контуру тока. Считается, что ток является линейным. Для объемных токов закон Био -- Савара-Лапласа записывается в несколько ином виде:
В формуле (2) интегрирование проводят по всем областям пространства, где присутствуют объемные токи, $\overrightarrow{j}$- плотность тока. Оба выражения (1) и (2) применимы только для постоянных токов.
Элементарная формулировка закона
Элементарном виде закон Био-Савара - Лапласа записывают соответственно:
где модуль элемента индукции магнитного поля равен:
или
Постоянные токи всегда замкнуты. Все наблюдаемые величины остались бы неизменными, если в правую часть формулы (3) добавить произвольное слагаемое, интеграл от которого по замкнутому контуру обращается в ноль. Из этого следует, что в рамках учения о постоянных токах элементарный закон Био -- Савара - Лапласа в формах (3) и (5) принципиально невозможно проверить опытным путем. Нельзя выделить на практике отдельные элементы постоянных токов и проводить с ними эксперименты. Опытной проверке можно подвергнуть только интегральные формы данного закона (1), (2).
Закон Био -- Савара -- Лапласа применяют для расчета магнитных полей. Векторы $d\overrightarrow{B},d\overrightarrow{l\ }и\ \overrightarrow{r}\ $ связаны правилом правого винта. Вектор $d\overrightarrow{B}$ перпендикулярен плоскости в которой находятся $d\overrightarrow{l\ }и\ \overrightarrow{r}$. В тех случаях, когда проводник с током и точка, где ищется поле, лежат в одной плоскости, все элементарные векторы поля направлены вдоль одной прямой. В остальных случаях $d\overrightarrow{B}$ не лежат не одной прямой. Магнитное поле элемента тока имеет осевую симметрию. Если магнитное поле имеет осевую симметрию, точка в которой ищут поле лежит на этой оси, то искомый вектор индукции магнитного поля направлен вдоль оси симетрии.
Полевая трактовка закона
Аналогично электростатике взаимодействие элементов тока представляют двумя стадиями.
- Один из элементов тока ($I_1dl_1$) создает магнитное поле в точке, где находится второй ток ($I_2dl_2$): \[d\overrightarrow{B_{12}}=\frac{{\mu }_0}{4\pi }\frac{I_1\left[d\overrightarrow{l_1}\overrightarrow{r_{12}}\right]}{{r_{12}}^3}\left(6\right).\]
- Второй элемент тока ($I_2dl_2$) взаимодействует с магнитным полем $d\overrightarrow{B_{12}}$, что ведет к возникновению силы $d\overrightarrow{F_{12}}:$ \[d\overrightarrow{F_{12}}=I_2dl_2\times d\overrightarrow{B_{12}}\ \left(7\right).\]
Задание: По плоскому контуру, который изображен на рис.1 течет постоянный ток силы I. Угол, между прямолинейными участками контура равен 900. Радиусы контуров $R_1$ и $R_2$. Какова магнитная индукция в точке C?
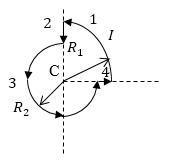
Рис. 1
Решение:
В точке С магнитное поле создают четыре проводника с током. Два из них прямолинейные, конечной длины, два являются частями витков с током.
В качестве основы для решения задачи используем закон Био -- Савара -- Лапласа в виде:
\[\overrightarrow{B}=\frac{{\mu }_0}{4\pi }\oint{\frac{I\left[d\overrightarrow{l}\overrightarrow{r}\right]}{r^3}}\left(1.1\right).\]Выделим в интеграле (1.1) четыре интеграла, по количеству участков -- проводников:
\[\overrightarrow{B}=\frac{{\mu }_0}{4\pi }\left(\int\limits_1{\frac{I\left[d\overrightarrow{l}\overrightarrow{r}\right]}{r^3}}+\int\limits_2{\frac{I\left[d\overrightarrow{l}\overrightarrow{r}\right]}{r^3}}+\int\limits_3{\frac{I\left[d\overrightarrow{l}\overrightarrow{r}\right]}{r^3}}+\int\limits_4{\frac{I\left[d\overrightarrow{l}\overrightarrow{r}\right]}{r^3}}\right)\left(1.2\right).\]В подынтегральном выражении мы имеем векторное произведение, модуль которого равен:
\[\left|d\overrightarrow{l}\times \overrightarrow{r}\right|=\left|d\overrightarrow{l}\right|\left|\overrightarrow{r}\right|{sin \left(\widehat{\overrightarrow{l}\overrightarrow{r}}\right)\ }\left(1.3\right).\]В таком случае, получим, что
\[\int\limits_2{\frac{I\left[d\overrightarrow{l}\overrightarrow{r}\right]}{r^3}}=0\ (1.4)\]так как для данного участка проводника $d\overrightarrow{l}\uparrow \downarrow \overrightarrow{r}$, следовательно, угол между этими векторами равен 1800, следовательно, $sin\pi =0.$
\[\int\limits_4{\frac{I\left[d\overrightarrow{l}\overrightarrow{r}\right]}{r^3}}=0(1.5).\]для данного участка проводника $d\overrightarrow{l}\uparrow \uparrow \overrightarrow{r}$, следовательно, угол между этими векторами равен 00, следовательно, $sin0=0.$
В соответствии с приведенными выше рассуждениями получаем, что поле в точке С можно найти как сумму двух интегралов:
\[\overrightarrow{B}=\frac{{\mu }_0}{4\pi }\left(\int\limits_1{\frac{I\left[d\overrightarrow{l}\overrightarrow{r}\right]}{r^3}}+\int\limits_3{\frac{I\left[d\overrightarrow{l}\overrightarrow{r}\right]}{r^3}}\right)\left(1.6\right).\]Или как сумму полей двух токов, которые текут в двух дугах окружностей. Для дуги окружности запишем:
\[r=R,\overrightarrow{dl}\bot \overrightarrow{R},\ sin\frac{\pi }{2}=1,\ sin\frac{d\alpha }{2}=\frac{dl}{2R},d\alpha -мал,sin\frac{d\alpha }{2}\approx \frac{d\alpha }{2}\ \to Rd\alpha =dl.\]Для части окружности с током элемент поля для точки в центре можно записать как:
\[dB=\frac{{\mu }_0I}{4\pi }\frac{R}{R^2}d\alpha =\frac{{\mu }_0I}{4\pi R}d\alpha (1.7),\]где ${\alpha }_1\le \alpha \le {\alpha }_2$.
Тогда для части окружности с радиусом $R_1$ запишем, что элемент поля в точке С равен:
\[B_1=\frac{{\mu }_0I}{4\pi R_1}\int\limits^{\frac{\pi }{2}}_0{d\alpha }=\frac{{\mu }_0\pi I}{8\pi R_1}\ \left(1.8\right)\]для части окружности с радиусом $R_2$ запишем, что элемент поля в точке С равен:
\[B_2=\frac{{\mu }_0I}{4\pi R_2}\int\limits^0_{\frac{\pi }{2}}{d\alpha }=-\frac{{\mu }_0\pi I}{8\pi R_2}\ \left(1.9\right).\]Результирующее поле равно:
\[\overrightarrow{B}=\frac{{\mu }_0I\overrightarrow{e_z}}{8}\left[\frac{1}{R_1}-\frac{1}{R_2}\right],\]где $\overrightarrow{e_z}$- единичный орт, направленный перпендикулярно плоскости чертежа.
Ответ: $\overrightarrow{B}=\frac{{\mu }_0I\overrightarrow{e_z}}{8}\left[\frac{1}{R_1}-\frac{1}{R_2}\right].$
Задание: Проводник имеет сечение формы тонкого полукольца с радиусом R. По нему течет ток силой I. Найдите индукцию магнитного поля в точках на оси полого полуцилиндра.
Решение:
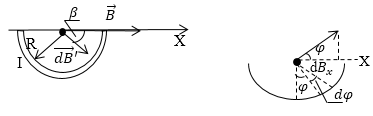
Рис. 2
Для решения задачи, данный проводник необходимо рассматривать как совокупность множества нитей с током, которые имею форму полуокружностей. Результирующая магнитная индукция будет направлена вдоль оси X (рис.2).
Индукцию одной нити будем искать с помощью закона Био -- Савара -- Лапласа.
Для части окружности с током элемент поля для точки в центре можно записать как:
\[dB'=\frac{{\mu }_0I}{4\pi }\frac{dlcos\varphi }{r^2}(2.1),\]где $cos\varphi =sin (\alpha )$, где $\alpha $ -- угол между элементом тока и радиус-вектором точки ($\overrightarrow{r}$), где ищем поле. Рассматривая треугольник, который построен на элементе dl, в котором можно записать:
\[l=rsin\varphi ,\ Rtg\varphi =l\to dl=R\frac{d\varphi }{{cos}^2\varphi }\] \[r=\frac{R}{cos\varphi }\left(2.2\right).\]Тогда в центре полуокружности одна нить с током создает магнитное поле с индуктивностью равной:
\[B'=\frac{{\mu }_0I}{4\pi }\int\limits^{\frac{\pi }{2}}_{-\frac{\pi }{2}}{\frac{Rcos\varphi d\varphi }{{cos}^2\varphi R^2}{cos}^2\varphi =\frac{{\mu }_0I}{4\pi }\int\limits^{\frac{\pi }{2}}_{-\frac{\pi }{2}}{\frac{cos\varphi d\varphi }{R}}=}\frac{{\mu }_0I}{4\pi R}sin{\left.\varphi \right|}^{\frac{\pi }{2}}_{-\frac{\pi }{2}}=\frac{{\mu }_0I}{2R}\left(2.3\right).\]Индукцию всего проводника найдем как:
\[B=\int\limits^{\pi }_0{dB'}sin\beta \left(2.4\right),\]где $dB'$- запишем как:
\[dB'=\frac{\mu_0dI}{2\pi R}\left(2.5\right).\]Элемент тока в нашем случае можно записать как:
\[dI=\frac{I}{l}dl=\frac{I}{l}Rd\beta \left(2.6\right).\]Подставим (2.6) в (2.5), за тем в (2.4), найдем искомую величину:
\[B=\int\limits^{\pi }_0{\frac{{\mu }_0IRd\beta }{2R\pi l}}sin\beta =\frac{{\mu }_0I}{2\pi l}\int\limits^{\pi }_0{sin\beta d\beta }=\frac{{\mu }_0I}{2\pi l}(-cos\beta )^{\pi }_0=\frac{{\mu }_0I}{\pi l}\left(2.7\right).\]Длина полуокружности равна:
\[l=\pi R\ \left(2.8\right).\]Ответ: $B=\frac{{\mu }_0I}{{\pi }^2R}.$











