Направление силы Ампера
Ампер первым установил, что проводники, по которым течет электрический ток, взаимодействуют механически (притягиваются или отталкиваются). Сила ($\overrightarrow{F}$), которая действует на прямолинейный проводник с током (I), всегда перпендикулярна проводнику и направлению вектора магнитной индукции ($\overrightarrow{B}$). В том случае, если прямолинейный проводник расположен параллельно вдоль направления линий магнитного поля, поле не действует. Конкретное направление силы Ампера можно найти с помощью правила левой руки. Левую руку надо расположить так, чтобы линии поля входили в ладонь, четыре пальца были направлены по току, тогда отогнутый на 90 градусов большой палец укажет направление силы Ампера. Если направление вектора $\overrightarrow{B}$ составляет некоторый угол с направлением тока, то для выяснения направления силы Ампера целесообразно разложить вектор магнитной индукции на две составляющие (рис.1):
где $\overrightarrow{B_{\bot }}$ - перпендикулярна току, $\overrightarrow{B_{II}}$ -- параллельна току. Только $\overrightarrow{B_{\bot }}$ - вызывает действие поля, к ней надо применять правило левой руки.
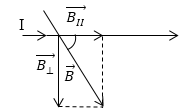
Рис. 1
Еще Ампер установил, что два параллельных проводника с током притягиваются, если токи имеют одинаковые направления и отталкиваются, если токи текут в противоположные стороны. Это просто объяснить, если представить, что один проводник создает магнитное поле, а другой проводник в него помещен и это поле действует на него. Можно использовать правило левой руки и выяснить, как направлена сила.
Закон Ампера
Для прямолинейного проводника сила Ампера имеет вид:
где $I$ -- сила тока, которая течет в проводнике, $\overrightarrow{B}$ -- вектор индукции магнитного поля, в которое проводник помещен, $\overrightarrow{l}$ -- длина проводника, направление задано, направлением тока. Модуль силы ампера в этом случае равен:
где $\alpha $ -- угол между векторами $\overrightarrow{l\ }и\ \overrightarrow{B}$.
Понятно, что на практике совсем не все проводники являются прямолинейными. Однако любой проводник можно разбить на совокупность частей, которые можно считать прямолинейными. Тогда вводится понятие элемента тока -- это величина равная$:\ Id\overrightarrow{l}$, где $d\overrightarrow{l}$ -- элементарный прямолинейный участок проводника, вектор, направленный по току. Тогда закон Ампера записывается в следующем виде:
В скалярном виде (4) запишем так:
где $\alpha $ -- угол между векторами $\overrightarrow{dl\ }и\ \overrightarrow{B}$.
Сила Ампера, действующая на провод с током конечной длины может быть найдена суммированием (векторным):
где интегрирование проводится по всей длине проводника.
Выражения (2) и (4) -- закон Ампера.
Для параллельных бесконечно длинных проводников с током сила Ампера имеет вид:
где $I_1,I_2$ -- токи, текущие в проводниках, $d$ -- расстояние между проводниками, $l$ -- длины проводников $(l\gg d)$, ${\mu }_0=4\pi \cdot {10}^{-7}\frac{Гн}{м}\ (Генри\ на\ метр)$ магнитная постоянная. Данная формула легко получается из закона Ампера.
Если один из проводников не является прямолинейным и надо найти силу Ампера, которая действует на него. Поле при этом создает прямой длинный проводник. Тогда искомую силу можно найти исход из формулы:
где $dF$ - сила Ампера, действующая на элементарный проводник с током ($I_2\overrightarrow{dl}$) со стороны бесконечно длинного прямолинейного проводника с током $I_1.$
Значение закона Ампера
На основании закона Ампера устанавливают единицы силы тока в системах СИ и СГСМ. Так как ампер равен силе постоянного тока, который при течении по двум параллельным бесконечно длинным прямолинейным проводникам бесконечно малого кругового сечения, находящихся на расстоянии 1м друг от друга в вакууме вызывает силу взаимодействия этих проводников равную $2\cdot {10}^{-7}Н$ на каждый метр длины.
Задание: В магнитном поле, направленном вертикально вниз на двух невесомых нитях горизонтально подвешен проводник с током силы I=2А. Масса проводника $m=10^{-2}$ кг, длина l=0,4м. Индукция магнитного поля равна 0,25Тл. Определите величину угла, на который отклонятся нити, на которых висит проводник с током. Проводник весь находится в поле.
Решение:
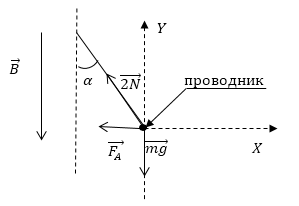
Рис. 2
Проводник расположен перпендикулярно плоскости рисунка (ток направлен от нас). Запишем условие равновесия для проводника:
\[\overrightarrow{F_A}+\overrightarrow{mg}+2\overrightarrow{N}=0\ \left(1.1\right),\]где $\overrightarrow{F_A}$- сила Ампера, $\overrightarrow{mg}$ -- сила тяжести, $\overrightarrow{N}$ -- сила реакции нити.
Проектируем (1.1) на оси:
\[X:\ -F_A-2Nsin\alpha =0\ \left(1.2\right).\] \[Y:\ -mg+2Ncos\alpha =0\ \left(1.3\right).\]Разделим (1.2) на (1.3), получим:
\[\frac{F_A}{mg}=tg\alpha \ \left(1.4\right).\]Модуль силы Ампера для прямолинейного проводника с током, который подвешен в поле с током, причем $\overrightarrow{B}\bot \overrightarrow{l}\ $равен:
\[F_A=IBl\ \left(1.5\right).\]Перепишем (1.4) с учетом (1.5), получим:
\[\frac{IBl}{mg}=tg\alpha \ \left(1.6\right).\]Подставим исходные данные, проведём вычисления:
\[tg\alpha =\frac{2\cdot 0,25\cdot 0,4}{10^{-2}\cdot 9,8}\approx 2\]Ответ: $\alpha \approx 64{}^\circ $.
Задание: Один проводник с током имеет форму квадрата, по нему утечет ток I. В одной плоскости с рамкой лежит бесконечно длинный прямой проводник с таким же током. Расположение проводников задано на рис.3. Найдите, какова сила, действующая на рамку, если расстояние между одной из сторон рамки и проводом равно длине стороны квадрата.
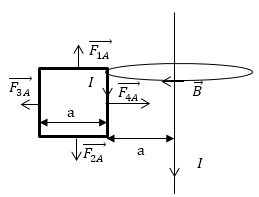
Рис. 3
Решение:
Магнитное поле создается бесконечно длинным проводником с током. Модуль индукции этого поля нам известен его можно записать как:
\[B\left(r\right)=\frac{{\mu }_0}{2\pi }\frac{I}{r}\left(2.2\right),\]где r -- расстояние от блинного проводника до точки поля.
Поле провода имеет цилиндрическую симметрию, для всех точек рамки оно будет направлено перпендикулярно. Если рассмотреть по очереди силы Ампера, которые действуют на каждый из четырех составных частей рамки, то выражение для модуля силы Ампера можно использовать в виде:
\[F=IBlsin\alpha \ \left(2.3\right),\]где $l=а$. Надо отметить, что на стороны, которые перпендикулярны проводнику с током будут действовать силы равные по модулю и противоположные по направлению, так результирующий их вклад равен нулю. $\overrightarrow{F_{1A}}$=-$\overrightarrow{F_{2A}}$.
Силы $F_{4A}\ и\ F_{3A}$ направлены вдоль одной прямой, но в противоположные стороны. Следовательно, результирующую силу по модулю найдем как:
\[F=F_{4A}-\ F_{3A}\left(2.4\right).\]Используя закон Ампера, и помня, что магнитное поле перпендикулярно току в сторонах квадрата, запишем:
\[F_{4A}=\frac{{\mu }_0}{2\pi }\frac{I^2}{a},\ F_{3A}=\frac{{\mu }_0}{2\pi }\frac{I^2}{2a}\left(2.5\right).\]Подставим (2.5) в (2.4), получим:
\[F=\frac{{\mu }_0}{2\pi }\frac{I^2}{a}-\ \frac{{\mu }_0}{2\pi }\frac{I^2}{2a}=\frac{{\mu }_0}{4\pi }\frac{I^2}{a}.\]Ответ: $F=\frac{{\mu }_0}{4\pi }\frac{I^2}{a}.$











