Вычисление амплитуды световых колебаний с использованием аналитического выражения принципа Гюйгенса - Френеля является в общем случае сложной, нетривиальной задачей. Однако Френель показал, что в некоторых случаях при наличии симметрии найти амплитуду суммарных колебаний можно используя алгебраическое или геометрическое суммирование.
Пусть сферическая или плоская волна попадает на экран с отверстием. Необходимо определить, как распределяется интенсивность света за экраном. Для того чтобы решить эту задачу используя принцип Гюйгенса - Френеля делают предположения:
-
Непрозрачные части экрана не работают как источники вторичных волн.
-
В отверстии экрана точки волнового фронта служат источником вторичных волн, как будто нет экрана.
Пусть точка А является источником сферической волны, $S$ - волновой фронт в момент времени $t$.
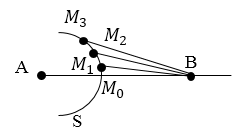
Рисунок 1.
Для того чтобы найти интенсивность волны в точке $В$, надо разбить поверхность $М$ на зоны - кольца, имеющие такие размеры, чтобы расстояния от краев зоны до точки $В$ были различны на величину $\frac{\lambda }{2}$. Границы зон на рис.1 обозначены как $M_0,\ M_1,\ M_2,\dots $ Запишем вышеназванное условие как:
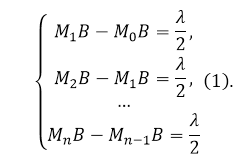
Рисунок 2.
Центральная зона носит название нулевой ($M_0$). Иногда центральную зону называют первой, при этом говорят, что $m=1,2,$ ...
Радиусы и площади зон Френеля
Для определения радиусов зон рассмотрим рисунок (рис. 2). На этом рисунке: радиусы зон $r_1,\ r_2,\dots ,r_m.$ $R$ - радиус кривизны сферического фронта волны. Точка $D$ обозначает место пересечения фронта волны с прямой $АВ$, $d_1,\ d_2,\dots ,d_m-$ расстояния от точки $D$ до проекции границы соответствующей зоны на прямую $АВ$. Из рис.2 видно, что для радиуса $r_m$ будет справедливо уравнение:
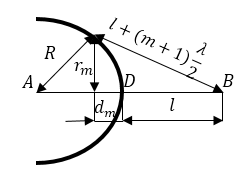
Рисунок 3.
Если ограничиться точностью величин до ${\lambda }^2$ из уравнения (2) следует:
Используя второе выражение из (3) площадь нулевой зоны найдем как:
Найдем суммарную площадь первой и нулевой зон, получим:
Соответственно площадь первой зоны равна:
Получилось, что площадь первой зоны равна площади нулевой зоны. Выражение (6) определяет площади и всех остальных зон. Пренебрегая кривизной поверхности фронта волны считают, что площадь кольцевой зоны на поверхности волнового фронта равна ее проекции на плоскость, которая перпендикулярна прямой $АВ$. Если радиусы зон Френеля существенно меньше радиуса кривизны волнового фронта, то ошибка в таком допущении небольшая. Если длины волн малы, из формулы (3) можно сделать вывод, что данное условие хорошо выполнимо для большого количества зон Френеля.
Амплитуды колебаний
Амплитуды колебаний, которые возбуждаются в точке В зонами Френеля образуют монотонно убывающую последовательность. При этом фазы колебаний, которые возбуждают соседние зоны отличны на $\pi $. Поэтому амплитуда результирующего колебания в точке В может быть записана как:
Запишем выражение (7) в ином виде:
Так как амплитуда ($A_m$) монотонно убывает, то приближенно можно положить, что:
В таком случае выражение (8) преобразуется до:
В соответствии с выражением (10) амплитуда волны в точке $В$ равна половине амплитуды волны, которая создается центральной зоной.
Задание: Длина волны, которую посылает точечный источник света, равна $\lambda=500нм$. Источник находится на расстоянии $a=1м$ от непроницаемого для света экрана с круглым отверстием диаметр его, равен $d=1\ мм$. Каким должно быть расстояние от экрана до точки, в которой ведутся наблюдения ($b$), если отверстие открывает три зоны Френеля?
Решение:
Будем считать, что центральная зона - первая, то есть $m=1,2,3$ ...
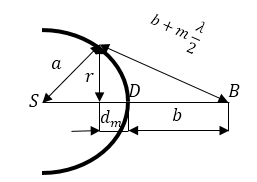
Рисунок 4.
Исходя из рис.4, можно записать:
\[r^2=a^2-{\left(a-d_m\right)}^2\left(1.1\right).\]Из численных данных задачи имеем, что:
\[\lambda \ll a,\ \to \lambda \ll b\left(1.2\right).\]Преобразуем выражение (1.1) к виду:
\[r^2={(b+m\frac{\lambda }{2})}^2-{\left(b+d_m\right)}^2\left(1.3\right).\]Выразим $d_m$, и $r^2$, учитывая, что выражение $\frac{b^2}{4{(a+b)}^2}m^2{\lambda }^2$мало, и им можно пренебречь, получим:
\[d_m=\frac{bm\lambda }{2(a+b)},\ r^2=\frac{ab}{a+b}m\lambda \left(1.4\right).\]Используя условие: $r=\frac{d}{2}$, из формулы для $r^2$ (1.4) найдем расстояние $b$:
\[b=\frac{ar^2}{am\lambda -r^2}\to b=\frac{ad^2}{4am\lambda -d^2}.\]Проведем вычисления, получим:
\[b=\frac{1\cdot {\left({10}^{-3}\right)}^2}{4\cdot 1\cdot 3\cdot 500\cdot {10}^{-9}-{\left({10}^{-3}\right)}^2}=0,2(м).\]Ответ: $0,2 м$.
Задание: Каким будет число зон Френеля, которые откроет отверстие радиусом r, если поле исследуется на расстоянии b от центра отверстия. Считать падающую волну плоской.
Решение:
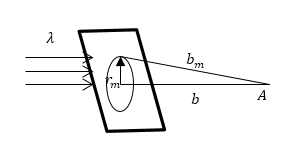
Рисунок 5.
Исходя из выражения, которое определяет зоны Френеля:
\[b_m=b+m\frac{\lambda }{2}(2.1)\]используя формулу для радиусов зон (рис.5):
\[{r_m}^2={b_m}^2-b^2\ \left(2.2\right)\]получим уравнение:
\[{r_m}^2={\left(b+m\frac{\lambda}{2}\right)}^2-b^2=b^2+2bm\frac{\lambda}{2}+{\left(m\frac{\lambda}{2}\right)}^2-b^2=bm\lambda+{\left(m\frac{\lambda}{2}\right)}^2\left(2.3\right).\]Так как длина волны видимого света мала, то ее квадратами можно пренебречь, то есть получаем:
\[{r_m}^2\approx bm\lambda \to m=\frac{{r_m}^2}{b\lambda }\left(2.4\right).\]Если по условию задачи радиус отверстия равен r, то искомая величина:
\[m=\frac{r^2}{b\lambda }.\]Ответ: $m=\frac{r^2}{b\lambda }.$











