Вектор потока электромагнитной энергии, определяемый как:
\[\overrightarrow{P}=\left[\overrightarrow{E}\overrightarrow{H}\right](1)\]называют вектором Умова - Пойнтинга (вектором Пойнтинга). Понятие вектора как потока энергии в разных веществах было введено Н.А. Умовым, а математическое выражение (1) получено Пойнтингом.
В электромагнитной волне векторы $\overrightarrow{E\ }\ и\ \overrightarrow{H}$ перпендикулярны, следовательно, модуль вектора $\overrightarrow{P}$ имеет выражение:
Направление вектора Умова - Пойнтинга перпендикулярно к векторам $\overrightarrow{E\ }и\ \overrightarrow{H}$, и со направленно с направлением распространения волны ($\overrightarrow{v}$).
Для плоской электромагнитной волны выражение для модуля вектора Умова - Пойнтинга имеет вид:
так как:
и между мгновенными значениями напряженности магнитного и электрического полей в электромагнитной волне существует соотношение:
откуда выражая напряженность магнитного поля, получаем:
Модуль вектора Умова -- Пойнтинга можно выразить как:
В диэлектрике объемная плотность электромагнитного поля равна:
Следовательно, сравнивая равенства (6) и (7), имеем:
В уравнения (2) -(8) входят мгновенные значения величин. Векторы в световой волне совершают колебания с частотами около ${10}^{15}Гц$, следовательно, весьма затруднительно следить за изменением величин во времени. Поэтому обращаются к средним значениям, переходя от мгновенных величин. Если электромагнитная волна является плоской, то среднее значение по времени вектора Умова - Пойнтинга равно:
Вектор Умова - Пойнтинга связан с энергией, которую несет электромагнитная волна соотношением:
где $\frac{\partial W}{\partial t}$ -- энергия, проходящая через площадку $S$ в единицу времени, $P_n=Pcos\alpha $ -- проекция вектора $\overrightarrow{P}$ на нормаль $\overrightarrow{n}$ к площадке $S$. Направление вектора Умова - Пойнтинга дает характеристику движения энергии в электромагнитном поле.
Если представить линии, касательные к которым в каждой точке совпадают с направлениями вектора $\overrightarrow{P}$, то такие линии есть пути распространения энергии электромагнитного поля. В оптике подобные линии называют лучами.
Теорема Пойнтинга
Для теории электромагнитных полей формулировки законов сохранения энергии и импульса имеет весьма важное значение. Теорема Пойнтинга - один из видов формулировок закона сохранения энергии: Скорость возрастания электромагнитной энергии внутри некоторого объема в сумме с энергией, которая вытекает за единицу времени через поверхность, ограничивающую тот же объем, равна полной работе, которую совершает поле над источниками внутри заданного объема, если взять ее со знаком минус.
Поясним данную формулировку. Выделим внутри некоторой среды объем $V$, который ограничивает поверхность $S$ (рис.1). Допустим, что полная энергия, которая заключена внутри объема, равна $W$. Тогда можно записать:
где $P_n$ -- нормальная составляющая вектора Умова - Пойнтинга. Интегрирование в (4) производят по всей замкнутой поверхности $S$. Положительным считают направление внешней нормали $\overrightarrow{n}$, что означает поток вектора $\overrightarrow{P}$ (выражение, которое стоит в формуле (4) в правой части) считают большим нуля, если линии потока энергии $\overrightarrow{P}$ выводят наружу из объема.
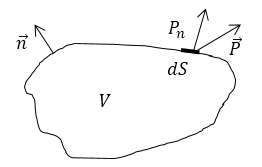
Рисунок 1.
При этом $-\frac{\partial W}{\partial t}$- величина, на которую уменьшатся, полная энергия внутри объема $V$ за единицу времени. По закону сохранения энергии она должна быть равна энергии, которая выходит через поверхность $S$ за единицу времени наружу. Следовательно, энергия, покидающая объем $V$ через поверхность $S$, выражена потоком вектора Умова - Пойнтинга.
Задание: Напишите выражение для вектора Умова - Пойнтинга, если энергию переносит волна, уравнение изменения вектора напряженности электрического поля которой задано как: $\overrightarrow{E}=10cos\left(\omega t-kx+\alpha \right)\overrightarrow{_z\ }(\frac{В}{м}).$ Учесть, что амплитуда вектора напряженности магнитного поля имеет вид: $H_m\overrightarrow{e_x}$, частота волны $\omega \ при\ ней\ \varepsilon =2,\ \mu \approx 1\ .$
Решение:
За основу решения задачи, примем определение вектора Умова - Пойнтинга:
\[\overrightarrow{P}=\left[\overrightarrow{E}\overrightarrow{H}\right]\left(1.1\right).\]Из условий видим, что колебания вектора напряженности электрического поля происходят по $оси Z$, колебания вектора напряженности магнитного поля по $оси X$, следовательно, вектор Умова - Пойнтинга колеблется по $оси Y$.
Модуль искомого вектора можно найти как:
\[P=EH\left(1.2\right).\]Найдем амплитуду вектора $\overrightarrow{H}$, если знаем, что амплитудные значения в нашем случае связаны соотношением:
\[\sqrt{\varepsilon {\varepsilon }_0}E_m=\sqrt{\mu {\mu }_0}H_m\left(1.3\right).\]Выразим из (1.3) искомую амплитуду $H_m$, имеем:
\[H_m=\sqrt{\frac{\varepsilon {\varepsilon }_0}{\mu {\mu }_0}}E_m\left(1.4\right).\]При этом уравнение колебаний вектора напряженности запишем в виде:
\[\overrightarrow{H}=\sqrt{\frac{\varepsilon {\varepsilon }_0}{\mu {\mu }_0}}E_mcos\left(\omega t-kx+\alpha \right)\overrightarrow{e_x\ }\left(1.5\right).\]Используя уравнения (1.1), (1.5) и уравнение колебаний вектора напряжённости электрического поля из условий задачи, запишем выражение для вектора Умова -- Пойнтинга:
\[P=\sqrt{\frac{\varepsilon {\varepsilon }_0}{\mu {\mu }_0}}{E_m}^2c{os}^2\left(\omega t-kx+\alpha \right)\left(1.6\right),\]где $\varepsilon =2,\ \mu =1,\ {\varepsilon }_0=\frac{1}{4\pi \cdot 9\cdot {10}^9}\frac{Ф}{м},\ {\mu }_0=4\pi \cdot {10}^{-7}\frac{Н}{А^2}$, следовательно:
\[{E_m}^2\sqrt{\frac{\varepsilon {\varepsilon }_0}{\mu {\mu }_0}}=100\cdot \sqrt{\frac{2}{4\pi \cdot {10}^{-7}\cdot 4\pi \cdot 9\cdot {10}^9}}=0,37.\]Ответ: $\overrightarrow{P}=\sqrt{\frac{\varepsilon {\varepsilon }_0}{\mu {\mu }_0}}{E_m}^2c{os}^2\left(\omega t-kx+\alpha \right)\overrightarrow{e_y}.$
Задание: Плоский конденсатор, имеющий круглые обкладки заряжен постоянным током за время $t_0$ до напряжения $U$. Расстояние между пластинами конденсатора равно $d$. Запишите выражение для вектора Умова - Пойнтинга для точек воображаемой цилиндрической поверхности радиуса $r$, которая находится между обкладками конденсатора. Считайте, что радиус пластин конденсатора много больше, чем радиус воображаемого цилиндра.
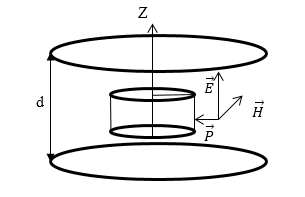
Рисунок 2.
Решение:
За основу решения задачи, примем определение вектора Умова -- Пойнтинга:
\[\overrightarrow{P}=\left[\overrightarrow{E}\overrightarrow{H}\right]\to P=EH\left(2.1\right).\]Переменное электрическое поле, возникающее в результате разрядки конденсатора, вызывает переменное магнитное поле. Запишем уравнение из системы Максвелла, учитывая, что между обкладками конденсатора токов проводимости нет:
\[rot\overrightarrow{H}=\frac{\partial \overrightarrow{D}}{\partial t}\left(2.2\right).\]и материальное уравнение:
\[\overrightarrow{D}=\varepsilon {\varepsilon }_0\overrightarrow{E}={\varepsilon }_0\frac{U}{d}\frac{t}{t_0}\overrightarrow{e_z}\left(2.3\right).\]Возьмем производную от $\overrightarrow{D}$ по времени:
\[\frac{\partial \overrightarrow{D}}{\partial t}=\varepsilon_0\frac{U}{d}\frac{1}{t_0}\overrightarrow{e_z}=rot\overrightarrow{H}\left(2.4\right).\]Возьмём интеграл от $rot\overrightarrow{H}$ по поверхности цилиндра радиуса $r$, применим теорему Стокса:
\[\int\limits_S{rot\overrightarrow{H}d\overrightarrow{S}}=\int\limits_S{\frac{\partial \overrightarrow{D}}{\partial t}d\overrightarrow{S}}=\oint\limits_L{\overrightarrow{H}d\overrightarrow{l}\left(2.5\right),}\]где
\[\oint\limits_L{\overrightarrow{H}d\overrightarrow{l}=2\pi rH\left(2.6\right),}\] \[\int\limits_S{\frac{\partial \overrightarrow{D}}{\partial t}d\overrightarrow{S}}=\varepsilon_0\frac{U}{d}\frac{1}{t_0}\pi r^2\left(2.7\right).\]Приравняем правые части выражений (2.6), (2.7), согласно тому, что выполняется (2.5):
\[2\pi rH=\varepsilon_0\frac{U}{d}\frac{1}{t_0}\pi r^2\to H=\frac{\varepsilon_0U}{2d}\frac{r}{t_0}\left(2.8\right).\]Найдем модуль вектора Умова -- Пойнтинга согласно выражениям (2.1) и (2.8):
\[P=\frac{U}{d}\frac{t}{t_0}\cdot \frac{{\varepsilon }_0U}{2d}\frac{r}{t_0}=\frac{{\varepsilon }_0r}{2}\frac{U^2}{d^2}\frac{t}{{t_0}^2}.\]Ответ: $P=\frac{\varepsilon_0r}{2}\frac{U^2}{d^2}\frac{t}{{t_0}^2}.$
Задание: Плоская электромагнитная волна распространяется в вакууме по $оси X$. Чему равна средняя энергия, которая проходит через единицу поверхности в единицу времени?
Решение:
сли мы имеем плоскую электромагнитную волну, то модули напряженности полей $\overrightarrow{E}\ $и $\overrightarrow{H}$ в произвольной точке $x$ могут быть выражены как:
\[E=E_0{sin \left(\omega t-kx\right)\ }\left(1.1\right),\] \[H=H_0{sin \left(\omega t-kx\right)\ }\left(1.2\right),\]где $k=\frac{2\pi }{\lambda }$. Следовательно, мгновенное значение вектора $\overrightarrow{P}$ можно записать в виде:
\[P=E_0{H_0{sin}^2 \left(\omega t-kx\right)\ }\left(1.3\right).\]По условию задачи волна распространяется в вакууме, следовательно, $\varepsilon =1,\ \mu =1\ $, имеем следующее соотношение между амплитудами полей:
\[\sqrt{{\varepsilon }_0}E_0=\sqrt{{\mu }_0}H_0\left(1.4\right).\]Кроме того, известно, что среднее значение $\left\langle {sin}^2\alpha \right\rangle =\frac{1}{2},$ тогда используем (1.3), (1.4) получаем среднее значение вектора Умова - Пойнтинга ($\left\langle P\right\rangle $) равно:
\[\left\langle P\right\rangle =\sqrt{\frac{{\varepsilon }_0}{{\mu }_0}}\frac{E^2_0}{2}.\]Ответ: Средняя энергия, которая проходит через единицу поверхности за единицу времени (интенсивность волны), равна $\left\langle P\right\rangle =\sqrt{\frac{{\varepsilon }_0}{{\mu }_0}}\frac{E^2_0}{2}.$
Задание: Вычислите среднее значение вектора Умова - Пойнтинга в стоячей волне.
Решение:
Колебания электрического и магнитного полей можно представить в стоячей волне с использованием следующих гармонических законов:
\[E=2E_0{cos \left(kx-\frac{{\varphi }_E}{2}\right)\ }{sin \left(\omega t-\frac{{\varphi }_E}{2}\right)\ }\left(2.1\right),\] \[H=2H_0{cos \left(kx-\frac{{\varphi }_H}{2}\right)\ }{sin \left(\omega t-\frac{{\varphi }_H}{2}\right)\ }\left(2.2\right),\]где ${\varphi }_E,\ \varphi_H$- запаздывание по фазе отраженной волны соответствующего поля, то есть:
\[{\varphi }_E=2\pi \frac{2l}{\lambda }+\theta (2.3),\] \[{\varphi }_H=2\pi \frac{2l}{\lambda }+ \vartheta(2.4),\]здесь $\theta ,\vartheta $ - изменение фазы при отражении, они равны или $\pi ,\ $или 0. $l-$длина линии (если рассматривается свободная волна, то это расстояние от излучателя до поверхности отражения). Обозначим:
\[2E_0{cos \left(kx-\frac{{\varphi }_E}{2}\right)\ }=E_1\left(2.5\right),\] \[2H_0{cos \left(kx-\frac{{\varphi }_H}{2}\right)\ }=H_1\left(2.6\right),\]тогда колебания, исходя из (2.1) и (2.2) в точке $x$ можно записать как:
\[E=E_1{sin \left(\omega t-\frac{{\varphi }_E}{2}\right)\ }\left(2.7\right),\] \[H=H_1{sin \left(\omega t-\frac{{\varphi }_H}{2}\right)\ }\left(2.8\right),\]при этом очевидно, что $E_1$ и $H_1$ не зависят от времени. Допустим, что $\theta =\pi $, тогда:
\[E=E_1{cos \left(\omega t-\frac{2\pi }{\lambda }l\right)\ }\left(2.9\right),\] \[H=H_1{sin \left(\omega t-\frac{2\pi }{\lambda }l\right)\ }\left(2.10\right).\]Исходя из (2.9) и (2.10), для вектора Умова - Пойнтинга получим:
\[P=E_1{cos \left(\omega t-\frac{2\pi }{\lambda }l\right)H_1{sin \left(\omega t-\frac{2\pi }{\lambda }l\right)\ }=\frac{E_1H_1}{2}\ }{sin \left(2\omega t-\frac{4\pi l}{\lambda }\right)\ }\left(2.11\right).\]Из формулы (2.11) следует, что колебания модуля вектора $\overrightarrow{P}$ происходят с частотой $2\omega $, при этом периодически изменяется знак. Следовательно, среднее значение вектора по времени равно $0$ ($\left\langle P\right\rangle =0$).
Ответ: В стоячей волне течения энергии нет, $\left\langle P\right\rangle =0$.












