Рассмотрим поведение плоских световых волн в анизотропной среде. Для этого используем уравнения:
Выразим из уравнения $(1.b)$ вектор $\overrightarrow{H}$ и подставим его в $\left(1.a\right)$, имеем:
где $v=\frac{\omega }{k}.$ Дальнейшие преобразования будем вести в декартовой системе координат, причем будем считать, что оси ее совпадают с главными осями тензора диэлектрической проницаемости, то есть:
В такой системе координат уравнение (2) примет вид трех скалярных уравнений:
Допустим, что вектор $\overrightarrow{E}\ $направлен по одной из главных диагоналей тензора диэлектрической проницаемости (например, $X$). В таком случае можно записать:
В этом случае уравнения (4) превращаются в одно уравнение:
где $v_1$ -- фазовая скорость, индекс 1 соответствует волне, у которой векторы $\overrightarrow{E}\ и\ \overrightarrow{D}$ коллинеарны оси $X$. Так как $E_1\ne 0$, то из уравнения (6) следует, что:
Аналогичными будут формулы для осей $Y$ и $Z$. То есть запишем:
$v_i$ называют главными скоростями распространения волны. Эти скорости не являются проекциями фазовой скорости волны на координатные оси, а характеризует фазовую скорость волны, векторы $\overrightarrow{E}\ и\ \overrightarrow{D}$ которой коллинеарны соответствующим осям. Учитывая выражение (7) векторное уравнение (2) можно представить:
Если умножить обе части уравнения (8) на $\frac{n_i}{1-\frac{v^2}{v^2_i}}$ и провести суммирование по i, то получим уравнение:
Учтем, что $\sum\limits_i{{n_i}^2=1}$, выражение (9) легко приводится к виду:
Формула (10)называется уравнением Френеля (уравнением волновых нормалей Френеля). С его помощью находят фазовую скорость в направлении $n_1,\ n_2,\ n_3.$ Уравнение (10)можно преобразовать к квадратному уравнению относительно фазовой скорости $v.$ Оно имеет два корня. Получается, что в любом направлении в анизотропной среде распространяются две волны с разными фазовыми скоростями ($v'и\ v''$), имеющими ортогональные поляризации ($D'\bot D''$). Получается, что при попадании световой волны в анизотропную среду она распадается на две волны, ортогонально поляризованные с разными скоростям и направлениями переноса энергии.
Уравнение (10) будет удовлетворяться, если в его левой части стоят слагаемые с разными знаками. Значит, $v^2\ $ни больше, ни меньше всех ${v_i}^2.$ Для того, чтобы найти корни уравнения (10) можно построить график функции $f(v^2)$ вида:
Такой график представлен на рис.1.
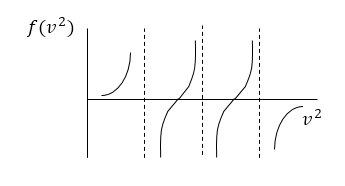
Рисунок 1.
На рис.1 пунктирные линии проводятся через точки ${v_i}^2.$ На рис.1 видно, что существуют два действительных значения ${v_i}^2$, которые удовлетворяют уравнению (10). Это значит, как уже говорилось, что в избранном направлении могут распространяться волны с двумя разными фазовыми скоростями $(v'и\ v''$), величины которых находятся между минимальной и средней, средней и максимальной из скоростей $v_i$.
Задание: В каждом направлении в анизотропном веществе могут распространяться две волны с разными фазовыми скоростями ($v'и\ v''$). Покажите, что их векторы электрического смещения перпендикулярны ($D'\bot D''$).
Решение:
В качестве основы для решения задачи используем уравнение:
\[\overrightarrow{n}\left(\overrightarrow{n}\cdot \overrightarrow{E}\right)-\overrightarrow{E}+{\mu }_0v^2\overrightarrow{D}=0\left(1.1\right)\]Запишем его дважды для $D',E'$ и $D'',E''$:
\[\overrightarrow{n}\left(\overrightarrow{n}\cdot \overrightarrow{E}'\right)-\overrightarrow{E'}+{\mu }_0{v'}^2\overrightarrow{D'}=0\left(1.2\right),\] \[\overrightarrow{n}\left(\overrightarrow{n}\cdot \overrightarrow{E''}\right)-\overrightarrow{E^{''}}+{\mu }_0{v''}^2\overrightarrow{D^{''}}=0\left(1.3\right).\]Умножим выражение (1.2) скалярно на $\overrightarrow{D^{''}}$, учтем, что ($\overrightarrow{n}\cdot \overrightarrow{D}=0$) получим:
\[\overrightarrow{E'}\overrightarrow{D^{''}}={\mu }_0v^{'2}\overrightarrow{D'}\overrightarrow{D^{''}}\left(1.4\right).\]Уравнение (1.3) умножим на $\overrightarrow{D'}$, получим:
\[\overrightarrow{E^{''}}\overrightarrow{D'}={\mu }_0v^{''2}\overrightarrow{D^{''}}\overrightarrow{D'}\left(1.5\right).\]Расписав в главных осях выражения $\overrightarrow{E'}\overrightarrow{D^{''}}$ получим:
\[\overrightarrow{E'}\overrightarrow{D^{''}}=\sum\limits_i{{E'}_i{\varepsilon }_0{\varepsilon }_i{E''}_i=\sum\limits_i{{E''}_i}}{\varepsilon }_0{\varepsilon }_i{E'}_i=\overrightarrow{E^{''}}\overrightarrow{D'}\left(1.6\right).\]Если левые части выражений (1.4) и (1.5) равны, то равны правые части:
\[{\mu }_0v^{'2}\overrightarrow{D'}\overrightarrow{D^{''}}={\mu }_0v^{''2}\overrightarrow{D^{''}}\overrightarrow{D'}\left(1.7\right).\]Проведем небольшие преобразования выражения (1.7), получим:
\[v^{'2}\overrightarrow{D'}\overrightarrow{D^{''}}-v^{''2}\overrightarrow{D^{''}}\overrightarrow{D'}=0\to \left(v^{'2}-v^{''2}\right)\overrightarrow{D'}\overrightarrow{D^{''}}=0\left(1.8\right).\]Так как $v^{'2}\ne v^{''2}$, то $\overrightarrow{D'}\overrightarrow{D^{''}}=0$, так как модули данный векторов отличны от нуля, следовательно, они перпендикулярны друг другу. Что следовало показать.
Задание: Существуют ли направления распространения световой волны в анизотропной среде, в которых фазовые скорости (решения уравнения волновых нормалей ($v'и\ v''$)) совпадают?
Решение:
Рассмотрим уравнение волновых нормалей Френеля:
\[\frac{{n_x}^2}{v^2-{v_x}^2}+\frac{{n_y}^2}{v^2-{v_y}^2}+\frac{{n_z}^2}{v^2-{v_z}^2}=0\ \left(2.1\right).\]Если избрать направление распространения волны, например таким, что:
\[{n_x}^2=\frac{{v_x}^2-{v_y}^2}{{v_x}^2-{v_z}^2},\ {n_y}^2=0,\ {n_z}^2=\frac{{v_y}^2-{v_z}^2}{{v_x}^2-{v_z}^2},\]два решения уравнения Френеля совпадают, что означает: $v'=v''$. Такие направления называют оптическими осями кристалла.
Ответ: Существуют (оптические оси кристаллов).












