Относительно простым прибором для реализации явления многолучевой интерференции служит пластинка Люммера – Герке. Это плоскопараллельная пластина, которая изготавливается из стекла (плавленого кварца), имеющего высокую однородность. Толщина пластинки колеблется от $3 мм$ до $20 мм$. Ее длина обычно составляет $30 см$. Для того, чтобы направлять лучи света конец имеет скос (рис.1) или на одном из концов пластинки находится небольшая призма (рис.2). В том и другом случае лучи, падающие на поверхность стекла перпендикулярны к ней, что позволяет уменьшать потери света при отражении. Направление падающих лучей подбирают таким, чтобы угол падения на границе стекло – воздух стал равен предельному углу полного отражения. В таком случае коэффициент отражения почти равен единице. Лучи претерпевают множественные отражения от плоскостей пластинки, интенсивность лучей, покидающих пластинку практически одинакова. Так получают до $10-15$ пучков с каждой стороны пластинки.

Рисунок 1.
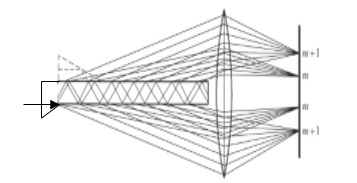
Рисунок 2.
Пластинка Люммера - Герке дает возможность наблюдать при интерференции полосы равного наклона. Условием для получения интерференционных максимумов является выражение:
где $l$ - толщина пластинки, $\Psi$ - угол преломления, $n$ - показатель преломления вещества пластинки. В данном случае мы не учитывали изменение фазы при отражении, так как оно не является существенным для смещения интерференционной картины. Количество интерферирующих пучков ($N$) можно вычислить в соответствии с формулой:
где $L$ - длина пластинки. По условию свет должен падать под предельным углом, тогда можно записать, что:
Пластинку Люммера - Герке применяют для изучения тонкой структуры спектральных линий. Используют ее в комбинации со вспомогательными диспергирующими приборами.
Пластинка Люммера - Герке изготовленная из кристаллического кварца прозрачна для длин волн до $2000$ ангстрем. Она долгое время была лучшим доступным интерферометром, имеющим большую разрешающую силу для спектроскопии ультрафиолетовых волн.
Дисперсионная область интерферометра Люммера - Герке
Пластинка Люммера - Герке относится к интерференционным спектроскопам. В ней интерферирующие пучки образуются в результате отражений света. Дисперсионная область спектроскопа для волн, падающего света, находящегося в интервале: от $\lambda \ до\ {\lambda }'=\lambda +\triangle \lambda $ определена формулой:
Получается, что при заданной длине волны дисперсионная область определена порядком спектра ($m$). Чем больше $m$, тем уже область дисперсии. Для интерферометра Люммера - Герке порядок спектра можно вычислить, используя формулу (1). Или заменив угол преломления, предельным углом отражения, получим:
В пластинке интерферируют пучки, чья интенсивность уменьшается с увеличением номера пучка. В том случае, если количество пучков можно было бы считать бесконечным, то в спектре содержались бы только главные максимумы. В действительности добавочные максимумы и минимумы в спектре присутствуют, так как число интерферирующих пучков ограничено.
Разрешающая способность пластинки Люммера - Герке
Разрешающей способностью (силой) спектрального устройства называют его возможность разделить две близкие по расположению спектральные линии.
Если в качестве минимальной разности длин волн, которые разделяет прибор взять $\delta \lambda $, то безразмерную величину, равную $\frac{\lambda }{\delta \lambda }$ называют разрешающей способностью ($\lambda $ - средняя длина волны двух разрешаемых линий). Тогда разрешающая способность пластинки Люммера - Герке вычисляется в соответствии с формулой:
Формула (6) хорошо согласуется с опытом, если угол выхода пучков света близок к $\frac{\pi }{2}$.
Для области дисперсии (лучи, выходят из пластинки под углом близким к скользящему углу) имеем:
Вследствие дисперсии показателя преломления стекла разрешающая способность пластинки Люммера - Герке растет, при этом область дисперсии уменьшается.
Задание: Оцените изменение разрешающей способности и области дисперсии пластинки Люммера - Герке, если 1) толщину пластинки увеличивают в два раза, а ее длину оставляют неизменной. 2) длину пластинки увеличивают в два раза, при этом не изменяют ее толщину.
Решение:
В качестве основы для решения задачи используем формулу, которая определяет разрешающую способность пластинки Люммера - Герке:
\[\frac{\lambda }{\delta \lambda }=L\left(\frac{n^2-1}{\lambda }-n\frac{dn}{d\lambda }\right)\left(1.1\right).\]Из этой формулы видно, что при $L=const\ (L\ -\ длина\ пластинки)$ и увеличении толщины пластинки ($l'=2l$), $\frac{\lambda }{\delta \lambda }$ не изменится.
Если $l=const$ (толщина пластинки не изменяется), увеличивается ее длина в два раза ($L'=2L$), то исходя из выражения для разрешающей способности (1.1), получаем, $\frac{\lambda }{\delta \lambda }$ увеличится в два раза.
Для ответа на вопрос относительно размера дисперсионной области используем формулу:
\[\triangle \lambda =\frac{{\lambda }^2}{2l\sqrt{n^2-1}\left(1-\frac{\lambda n}{n^2-1}\frac{dn}{d\lambda }\right)}\left(1.2\right).\]Из выражения (1.2) очевидно, что область дисперсии не зависит от длины пластины и обратно пропорциональна ее толщине, соответственно при $L=const,\ l'=2l$ дисперсионная область уменьшится в два раза. В случае если $l=const,\ $а $L'=2L$ область дисперсии не изменится.
Ответ: 1) $\frac{\lambda }{\delta \lambda }=const$, $\triangle \lambda'=\frac{1}{2}\triangle \lambda $. 2) ${\left(\frac{\lambda }{\delta \lambda }\right)}'=2(\frac{\lambda }{\delta \lambda })$, $\triangle \lambda'=const$.
Задание: Вычислите, чему должна быть равна минимальная длина пластинки Люммера - Герке, для того чтобы разрешить дублетную структуру линии водорода $H_{\alpha }$, если показатель преломления вещества пластинки ($n$) равен 1,5, средняя длина волны ($\lambda $) равна $656,3\ нм\ =656,3\cdot {10}^{-9}м$, разность длин волн ($\delta \lambda $) равна 0,014 нм=$0,014\ \cdot {10}^{-9}м$, а отношением $\frac{dn}{d\lambda }$ можно пренебречь.
Решение:
Как основу для решения задачи используем формулу:
\[\frac{\lambda }{\delta \lambda }=L\left(\frac{n^2-1}{\lambda }-n\frac{dn}{d\lambda }\right)\left(2.1\right).\]Из условий задачи величиной $\frac{dn}{d\lambda }$ можно пренебречь, следовательно, выражение (2.1) преобразуем к виду:
\[\frac{\lambda }{\delta \lambda }=L\frac{n^2-1}{\lambda }\left(2.2\right).\]Выразим из формулы (2.2) длину пластинки, получим:
\[L=\frac{{\lambda }^2}{\delta \lambda (n^2-1)}.\]Вычислим искомую величину:
\[L=\frac{{\left(656,3\cdot {10}^{-9}\right)}^2}{0,014\ \cdot {10}^{-9}({1,5}^2-1)}=\frac{430729,7\cdot {10}^{-18}}{0,0175\cdot {10}^{-9}}=2,5\cdot {10}^{-2}\left(м\right).\]Ответ: $L=2,5\ см.$












