Метод Юнга
Первым, кто сконструировал установку для демонстрации явления интерференции световых волн, был Т. Юнг. Источником света в его опыте была узкая щель, которая освещалась ярким светом ($S$). От нее свет падал на две узкие щели $S_1\ и\ S_2$, которые параллельны $S$ и находятся от нее на равном расстоянии (рис.1). Щели $S_1\ и\ S_2$ становятся когерентными источниками света.
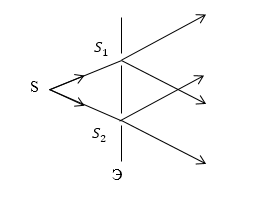
Рисунок 1.
При этом интерференционная картина наблюдается в плоскости $XOY$, перпендикулярной к нормали $CO$, проведенной к середине отрезка, который соединяет точки, в которых находятся вторичные источники света (рис.2).
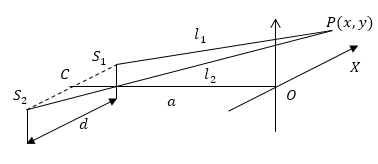
Рисунок 2.
Для точки P(x,y) (рис.2), которая находится в плоскости наблюдения, имеем:
Из формул (1) и (2) следует:
Разность путей света от источников до точки P можно записать как:
Система максимумов (минимумов) будет наблюдаться только в случае, если $d\ll a$. Если $x,\ y\ll a$, то:
В таком случае имеем:
Оптическая разность хода, следовательно, равна:
При этом разность фаз представлена формулой:
Так как угол $S_1PS_2$ мал, то часто считают, что волны от обоих источников движутся по одному направлению, максимумы интенсивности в таком случае будут при:
минимумы при:
Так, интерференционная картина около точки $О$ (рис.2) состоит из интерференционных полос, которые лежат на одинаковых расстояниях и направлены под прямым углом к линии $S_1S_2$.
Зеркала Френеля
Одним из способов получить когерентные источники света служит устройство, которое называют зеркалами Френеля. В этом устройстве свет от точёного источника $S$ падает на два плоских зеркала $З_1$ и $З_2$, которые расположены под малым углом друг к другу ($\alpha $). При отражении свет образует два мнимых когерентных источника $S_1$ и $S_2\ (рис.3).$ Плоскость $SS_1S_2$, перпендикулярна к линии пересечения зеркал, $A$ -- точка пересечения. Если расстояние $SA=b$, то $S_1A=S_2A=b.$ Перпендикуляр к середине отрезка $S_1S_2$ проходит через точку $А$. Расстояние между $S_1$ и $S_2$ равно:
При этом ширина полосы интерференции ($\triangle x$) равна:
где $a$ -- расстояние от точки А до экрана (рис.3).
Максимальное количество интерференционных полос ($N$) равно:
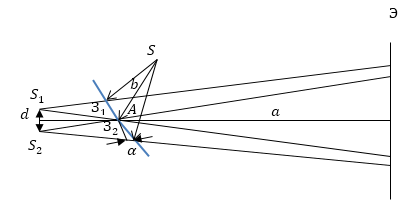
Рисунок 3.
Бипризма Френеля
Бипризма состоит из двух призм, имеющих малые преломляющие углы ($\vartheta$). Эти призмы сложены так, что имеют одну общую грань. Источник света ($S$) расположен параллельно этой общей грани на некотором расстоянии ($a$) от нее. Свет, испускаемый источником, преломляется обеими призмами. В результате за призмой распространяется свет как бы исходящий от мнимых когерентных источников $S_1\ и\ S_2$, которые лежат в той же плоскости, что и $S$ (рис.4). В результате на поверхности экрана происходит наложение когерентных волн и возникает явление интерференции.
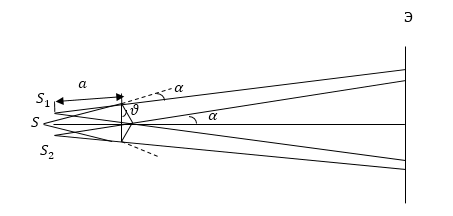
Рисунок 4.
В данном случае $\triangle x$ равно:
где n -- показатель преломления призмы, $l$- расстояние от источников света до экрана.
Максимальное количество интерференционных полос ($N$) равно:
Во всех подобных устройствах с первичным точечным источником интерференционные полосы наблюдаются в монохроматическом свете в любой области перекрытия расходящихся пучков от источников $S_1\ и\ S_2$. Про такие полосы говорят, что они не локализованы.
Задание: Опишите, что собой представляет зеркало Ллойда.
Решение:
С помощью системы, называемой зеркалом Ллойда, получают когерентные источники света (рис.5). Точечный источник $S_1$ помещают на расстоянии $a$ от плоского зеркала (З), близко к его поверхности. При этом считается, что свет отражается под углом близким к скользящему углу. В качестве когерентных источников выступают первичный источник $S_1\ $и его мнимое изображение в зеркале $S_2$. Надо отметить, что перпендикуляр к середине отрезка $S_1S_2$ лежит в плоскости зеркала.
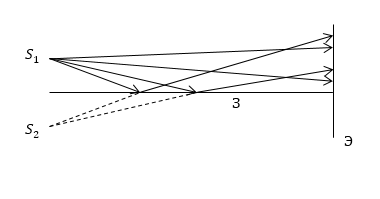
Рисунок 5.
Задание: Что собой представляет билинза Бийе.
Решение:
Билинза Бийе составлена из выпуклой линзы, которая разрезана по диаметру на две части. Эти части слегка раздвинуты в направлении, перпендикулярном оптической оси. Благодаря этой линзе образуются два действительных изображения ($S_1\ и\ S_2$) источника световой волны ($S$). Интерференционные полосы образуются в области перекрытия расходящихся пучков света от источников.
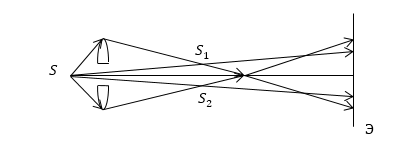
Рисунок 6.












