Степень поляризации света
Волна света, испускаемая элементарным источником (атомом или молекулой) в любом акте излучения является поляризованной. Однако макроскопические источники света (светящиеся тела или отражающие) имеют большое количество элементарных излучателей, световые векторы которых ориентированы в пространстве хаотично, моменты актов испускания света также не имеют согласований. Следовательно, суммарное направление вектора напряженности при излучении макротелом не предсказуемо. Данный свет называют неполяризованным. Различают неполяризованный, полностью поляризованный и частично поляризованный свет.
Характеристикой света, имеющего частичную поляризацию, является ее степень (P). Которую определяют как:
где $I_{max},I_{min}$ -- максимальные и минимальные интенсивности света, наблюдаемые при поляризации и относимые к двум взаимно перпендикулярным составляющим светового вектора. Свет, который испускают реальные источники, всегда не поляризован или поляризован частично Часто для естественного света $I_{max}=I_{min}$, значит $P=0$. Для света, имеющего плоскую поляризацию $I_{min}=0$, следовательно, $P=1$. Естественный свет преобразуют в поляризованный, применяя поляризаторы. Эти устройства пропускают колебания только определенных направлений колебания.
Монохроматическое векторное поле всегда в общем случае имеет эллиптическую поляризацию. Напомним, что векторное поле называют монохроматическим, если его три проекции на оси координат выполняют гармонические колебания с одинаковыми частотами частотой, запишем их как:
В векторной форме данное поле можно представить как:
Если векторы $\overrightarrow{A_1}\left(\overrightarrow{r}\right)$ и $\overrightarrow{A_2}\left(\overrightarrow{r}\right)$ коллинеарны, то в этих точках вектор напряженности им параллелен (волна поляризована линейно). В случае не коллинеарности векторов $\overrightarrow{A_1}\left(\overrightarrow{r}\right)$ и $\overrightarrow{A_2}\left(\overrightarrow{r}\right)$ вектор $\overrightarrow{E}$ лежит в плоскости этих векторов и его конец описывает плоскую кривую. Для нахождения формы этой кривой следует сложить два взаимно перпендикулярные гармонические колебания одной частоты, сдвинутые по фазе относительно друг друга. Из такого сложения получается движение конца вектора напряженности по эллипсу.
Закон Малюса
Колебания амплитуды $A$, которое совершается в плоскости, имеющей с плоскостью поляризатора угол $\alpha $ можно разложить на две составляющие:
Первое колебание пройдет через поляризатор, второе задержано. Интенсивность волны прошедшей пропорциональна квадрату ее амплитуды:
где $I$ -- интенсивность колебаний с амплитудой $A$. Значит, доля интенсивности, которую несет колебание, параллельное плоскости поляризатора, равна $cos^2\alpha .$ В естественном свете все значения $\alpha $ имеют равную вероятность. Следовательно, доля света, который прошел сквозь прибор, есть среднее $cos^2\alpha $, то есть: $\left\langle cos^2\alpha \right\rangle =\frac{1}{2}.$
Если вращать поляризатор вокруг направления луча естественного света, интенсивность света, который прошел через поляризатор изменяться не будет. При этом меняется только ориентация плоскости колебаний света, покидающего прибор.
Допустим, что на поляризатор попадает плоско поляризованный свет, имеющий амплитуду $A_0$, при этом его интенсивность $I_0$ (рис.1).
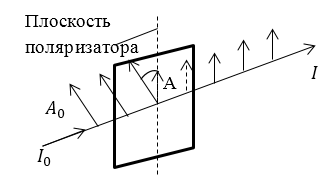
Рисунок 1.
Через поляризатор распространится часть колебаний с амплитудой:
где $\alpha $ -- угол между плоскостью колебаний падающей волны света и плоскостью поляризатора. В таком случае, интенсивность света, который прошел сквозь поляризатор, определена уравнением:
Этот закон именуется законом Малюса.
Пусть на пути луча естественного света расположены два поляризатора. Плоскости данных поляризаторов расположены под углом $\alpha $. После прохождения сквозь первый поляризатор луч света будет плоско поляризованным, его интенсивность обозначим $I_0$, она составляет половину интенсивности естественного света ($I_{est}$). В соответствии с законом Малюса из второго поляризатора свет выйдет, имея интенсивность $I_0cos^2\alpha .\ \ $Следовательно, интенсивность света, прошедшего через два поляризатора равна:
Задание: Какова степень поляризации ($P$) света, если в его составе присутствует естественный свет и плоско поляризованный, при этом интенсивность поляризованного света ($I_p$) в 4 раза больше, чем интенсивность естественного света ($I_{est}$)?
Решение:
В качестве основы для решения задачи используем определение степени поляризации:
\[P=\frac{I_{max}-I_{min}}{I_{max}+I_{min}}\left(1.1\right),\]где:
\[I_{max}=I_p+\frac{1}{2}I_{est}\left(1.2\right).\] \[I_{min}=\frac{1}{2}I_{est}\left(1.3\right).\]Используя условия задачи можно записать, что:
\[I_{max}=4I_{est}+\frac{1}{2}I_{est}=4,5\ I_{est}\left(1.4\right).\]Подставим полученное из формул (1.3) и (1.4) в выражение (1.1), имеем:
\[P=\frac{(4,5-0,5)I_{est}}{(4,5+0,5)\ I_{est}}=0,8.\]Ответ: $P=0,8$.
Задание: Каково будет изменение интенсивности света, который прошел через поляризатор и анализатор, если угол между ними равен ${\alpha }_2=\frac{\pi }{4}?$ При этом угол между главными плоскостями поляризатора и анализатора равен ${\alpha }_1=\frac{\pi }{6}$.
Решение:
Как основу для решения задачи используем закон Малюса:
\[I=I_0cos^2\alpha \left(2.1\right).\]Запишем его для ${\alpha }_1$:
\[I_1=I_0cos^2{\alpha }_1\left(2.2\right)и\ \]для ${\alpha }_2$:
\[I_2=I_0cos^2{\alpha }_2\left(2.3\right).\]Используя выражения (2.2) и (2.3), найдем искомое отношение ($\frac{I_1}{I_2}$):
\[\frac{I_1}{I_2}=\frac{I_0cos^2{\alpha }_1}{I_0cos^2{\alpha }_2}=\frac{cos^2{\alpha }_1}{cos^2{\alpha }_2}\ \left(2.4\right).\]Подставим данные условий задачи в выражение (2.4), проведем вычисления:
\[\frac{I_1}{I_2}=\frac{cos^2\frac{\pi }{6}}{cos^2\frac{\pi }{4}}=\frac{{\left(\frac{\sqrt{3}}{2}\right)}^2}{{\left(\frac{1}{\sqrt{2}}\right)}^2}=1,5.\]Ответ: Изменится в $1,5$ раза.











