В интерферометре Майкельсона используется явление интерференции в тонких пленках. Явление интерференции в данном приборе осуществляется способом деления амплитуды волны.
Что собой представляет это устройство? На массивном постаменте находится плоскопараллельная слегка покрытая серебром пластинка ($A$), расположенная под углом $45^0$ к направлению распространения лучей и два взаимно перпендикулярных плоских зеркала $C$ и $D$ (рис.1).
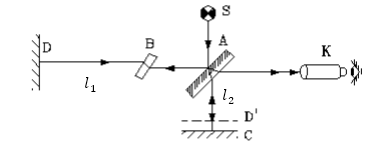
Рисунок 1.
Пластина B (рис.1) служит как вспомогательная, она компенсирует разность хода лучей. Световые волны распространяются от источника света ($S$). Часть из них отражается от серебряной поверхности пластины $A$, часть проходит сквозь данную пластинку. Так происходит процесс расщепления волны света на две когерентные волны. Волны, которые проходят через пластинку отражаются от зеркал $C$ и $D$. Отраженные волны снова частично отражаются, частично проходят сквозь посеребрённую пластинку $A$. Эти волны могут интерферировать на участке $АК$. Эта интерференционная картина наблюдается в зрительную трубу. Так, на пластинке $А$ происходит деление амплитуды, фронт волн на ней сохраняется изменяется только направление его движения.
Если гипотетически плечо $DA$ развернуть на $90^0$, то зеркало $D$ попадет в положение $D'$. Между $D'$ и $С$ появляется промежуток, который может быть подобен тонкой пленке. В том случае, если зеркала $C$ и $D$ строго перпендикулярны, то наблюдаются полосы равного наклона, которые представляют собой круги. Зрительная труба в таком случае должна быть настроена на бесконечность. Если зеркала $C$ и $D$ не совсем перпендикулярные, то промежуток между нами уподобляется клину, то появляются полосы равной толщины в виде прямых полос. Зрительную трубу в этом случае фокусируют на посеребренную грань пластинки $А$.
Интерференция монохроматических волн, которые распространяются по оси интерферометра
В случае распространения волн строго по оси интерферометра оптическая разность хода лучей ($\triangle $) появляется за счет разницы в длинах плечей ($l_1\ и\ l_2\ \ $) интерферометра:
Появляющаяся при этом разность фаз равна:
При строгом расчете следует учесть изменение фаз волн при отражении от зеркал и преломления в пластинке $A$, здесь мы этого делать не будем, так как принципиального значения для картины интерференции это в нашем случае не имеет.
Будем считать, что при каждом попадании волны на пластину $A$ плотность потока энергии делится на две части. Опишем волны, идущие в направлении зрительной трубы уравнениями:
где $E_0$ -- амплитуда волны до попадания на пластинку $А$. $\delta ={\varphi }_2-{\varphi }_1$. Следовательно, для наблюдаемой в результате интенсивности получим:
где $I_0=\frac{1}{2}{E_0}^2$ -- интенсивность входящей от источника света волны.
В том случае, если:
интенсивность (3) равна нулю. Если:
интенсивность равна $I_0$, что означает: вся энергия от источника попадает на «экран», потока энергии, которая возвращается в направлении источника света, нет.
Интерферометр Майкельсона применяют для измерения маленьких расстояний, малых изменений показателей преломления. Сам Майкельсон применял свой интерферометр для опыта, по проверке связи скорости света с направлением движения луча по отношению к Земле.
Задание: Для того чтобы вычислить показатель преломления аммиака в одно плечо интерферометра Майкельсона помещается стеклянная трубка внутри которой находится вакуум. Ее длина $l=15\ см=15\cdot 10^{-2}м$. В случае заполнения данной трубки аммиаком интерференционная картина для длины волны равной $\lambda =589\ нм=589\cdot {10}^{-9}м$ смещается на $192$ полосы. Чему равен показатель преломления аммиака?
Решение:
Разность оптического хода волны ($\triangle $) в вакууме и аммиаке можно найти как:
\[\triangle =ln-ln_v\left(1.1\right),\]где $n_v$=1 показатель преломления для вакуума. Запишем условие интерференционных минимумов:
\[\triangle =m\frac{\lambda }{2}\ \left(m=0,\pm 1,\pm 2,\dots \right)\left(1.2\right).\]Приравняем правые части выражений (1.1) и (1.2), получим:
\[ln-l=m\frac{\lambda}{2}\left(1.3\right).\]Выразим из (1.3) показатель преломления:
\[n=m\frac{\lambda }{2l}+1\left(1.4\right).\]Проведем вычисления:
\[n=192\cdot \frac{589\cdot {10}^{-9}}{2\cdot 15\cdot 10^{-2}}+1\approx 1,000377.\]Ответ: $n=1,000377.$
Задание: В интерферометре Майкельсона при поступательном движении одного из зеркал интерференционная картина то исчезает, то появляется. Каково перемещение ($\triangle l$) зеркала между двумя последовательными появлениями четкой интерференционной картины, если использовать волны ${\lambda }_1$ и ${\lambda }_2$?
Решение:
Причиной исчезновения интерференционной картины можно считать то, что максимумы и минимумы интерференционной картины волн разной длины сдвинуты относительно друг друга. При достаточной разнице в длине волны максимумы в интерференции одной волны могут попадать на минимумы другой, тогда интерференционная картина полностью исчезает.
Запишем условие перехода от одной четкой картины к другой:
\[\left(z+1\right){\lambda }_1=z{\lambda }_2\left(2.1\right),\]где $z$ -- целое число. Искомое перемещение зеркала ($\triangle l$) можно определить как:
\[2\triangle l=z{\lambda }_2\left(2.2\right).\]Используя систему уравнений (2.1) и (2.2) выразим $\triangle l$:
\[\left(z{\lambda }_1+{\lambda }_1\right)=z{\lambda }_2\to z{(\lambda }_2-{\lambda }_1)={\lambda }_1\to z=\frac{{\lambda }_1}{{(\lambda }_2-{\lambda }_1)},\] \[\triangle l=\frac{{\lambda }_1{\lambda }_2}{2{(\lambda }_2-{\lambda }_1)}.\]Ответ: $\triangle l=\frac{{\lambda }_1{\lambda }_2}{2{(\lambda }_2-{\lambda }_1)}.$











