Допустим, что граница раздела сред плоская и неподвижная. На нее падает плоская монохроматическая волна:
отражённая волна при этом имеет вид:
для преломленной волны имеем:
отраженная и преломленная волны будут тоже плоскими, и иметь ту же частоту: ${\omega }_{pad}=\omega_{otr}=\omega_{pr}=\omega $. Равенство частот следует из линейности и однородности граничных условий.
Разложим электрическое поле каждой волны на две компоненты. Одну, находящуюся в плоскости падения, другая в перпендикулярной плоскости. Эти составляющие называют главными составляющими волн. Тогда можно записать:
где ${{\overrightarrow{e}}_x,\overrightarrow{e}}_y,\ {\overrightarrow{e}}_z$ -- единичные векторы вдоль осей $X$,$Y$,$Z.$ ${\overrightarrow{e}}_1,\ {\overrightarrow{e}}'_1,{\overrightarrow{e}}_2$ -- единичные векторы, которые находятся, в плоскости падения и перпендикулярны соответственно, падающему, отраженному и преломленному лучам (рис.1). То есть можно записать:
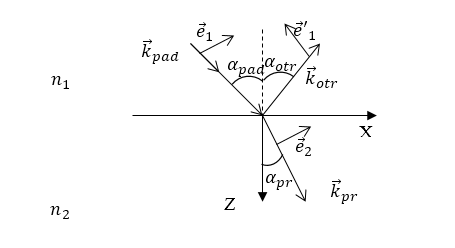
Рисунок 1.
Скалярно умножим выражение (2.а) на вектор ${\overrightarrow{e}}_x,$ получаем:
Аналогичным путем получают:
Так, выражения (4) и (5) дают $x-$, $y-$. $z-$ составляющие электрического поля на границе раздела веществ (при $z=0$). Если не учитывать магнитных свойств вещества ($\overrightarrow{H}\equiv \overrightarrow{B}$), то компоненты магнитного поля можно записать как:
Соответствующие выражения для отраженной волны имеют вид:
Для преломленной волны:
Для нахождения $E_{pr\bot }$,$\ E_{pr//},\ E_{otr\bot },\ E_{otr//}$ используют граничные условия:
Подставим в выражения (11) формулы (10), получим:
Из системы уравнений (12),учитывая равенство угла падения и угла отражения (${\alpha }_{pad}=\alpha_{otr}=\alpha $) получим:
Отношения, которые стоят в левых частях выражений (13) называют коэффициентами Френеля. Данные выражения формулами Френеля.
При обычном отражении коэффициенты Френеля вещественные. Это доказывает, что отражение и преломление не сопровождает изменение фазы, исключение -- изменение фазы отраженной волны на $180^\circ$. В том случае, если падающая волна является поляризованной, то отраженная и преломленная волны тоже поляризованы.
Получая формулы Френеля, мы полагали свет монохроматическим, однако, если среда не является диспергирующей и происходит обычное отражение, то данные выражения справедливы и для немонохроматических волн. Надо только под составляющими ($\bot $ и //) понимать соответствующие компоненты напряженностей электрического поля падающей, отраженной и преломленной волн на границе раздела.
Задание: Объясните, почему изображение заходящего солнца при тех же условиях не уступает по яркости самому солнцу.
Решение:
Для объяснения подобного явления используем следующую формулу Френеля:
\[\frac{E_{otr\bot }}{E_{pad\bot }}=-\frac{sin (\alpha -{\alpha }_{pr})}{sin (\alpha +{\alpha }_{pr})};\ \frac{E_{otr//}}{E_{pad//}}=\frac{tg (\alpha -{\alpha }_{pr})}{tg (\alpha +{\alpha }_{pr})}(1.1).\]В условиях скользящего падения, когда угол падения ($\alpha $) практически равен $90^\circ$ получаем:
\[\frac{E_{otr\bot }}{E_{pad\bot }}=\frac{E_{otr//}}{E_{pad//}}\to -1(1.2).\]При скользящем падении света коэффициенты Френеля (по модулю) стремятся к единице, то есть отражение получается практически полным. Это объясняет яркие изображения берегов в спокойной воде водоема и яркость заходящего солнца.
Задание: Получите выражение для отражательной способности ($R$), если так называют коэффициент отражения при нормальном падении света на поверхность.
Решение:
Для решения задачи используем формулы Френеля:
\[\frac{E_{otr\bot }}{E_{pad\bot }}=\frac{n_1cos\left(\alpha \right)-n_2cos\left({\alpha }_{pr}\right)}{n_1cos\left(\alpha \right)+n_2cos\left({\alpha }_{pr}\right)},\ \frac{E_{otr//}}{E_{pad//}}=\frac{n_2{cos \left(\alpha \right)\ }-n_1{cos \left({\alpha }_{pr}\right)\ }}{n_2{cos \left(\alpha \right)\ }+n_1{cos \left({\alpha }_{pr}\right)\ }}\left(2.1\right).\]При нормальном падении света формулы упрощаются и превращаются в выражения:
\[\frac{E_{otr\bot }}{E_{pad\bot }}=-\frac{E_{otr//}}{E_{pad//}}=\frac{n_1-n_2}{n_1+n_2}=\frac{n-1}{n+1}(2.2),\]где $n=\frac{n_1}{n_2}$
Коэффициентом отражения называют отношение энергии отраженной к энергии падающей. При этом известно, что энергия пропорциональна квадрату амплитуды, следовательно, можно положить, что искомый коэффициент можно найти как:
\[R={\left(\frac{n-1}{n+1}\right)}^2.\]Ответ: $R={\left(\frac{n-1}{n+1}\right)}^2.$












