Обыкновенный и необыкновенный лучи
Луч называют необыкновенным, если у него электрический вектор $\overrightarrow{E_e}$ находится в главной плоскости, его скорость зависит от направления (главная ось в сечении эллипсоида меняется при изменении направления луча). Параметры, которые будут относиться к данному лучу, будем обозначать индексом $e$.
У отрицательных кристаллов имеем соотношение скоростей: $v_0v_{e.}$
Сущность двойного лучепреломления
Так как внутри кристалла является возможным распространение с различными лучевыми скоростями двух лучей, то преломление на поверхности ведет к появлению двух лучей внутри тела. Такое разделение луча, который входит в кристалл, называют двойным лучепреломлением.
Данное явление открыто в $1669$ г. Э. Бартолинусом и пояснено Х. Гюйгенсом.
Характерные случаи двойного лучепреломления
Допустим, что оптическая ось перпендикулярна поверхности кристалла. В случае перпендикулярного падения луч будет направлен по оптической оси, значит, он распространяется как будто в изотропной среде, следовательно, двойное лучепреломление отсутствует. Пусть луч падает под углом к поверхности кристалла. В таком случае двойное лучепреломление можно наблюдать и оно зависит от типа кристалла. В отрицательном кристалле обыкновенный луч преломляется сильнее необыкновенного (рис.1($a$)). В положительном кристалле больше преломляется необыкновенный луч (рис.1($b$)).
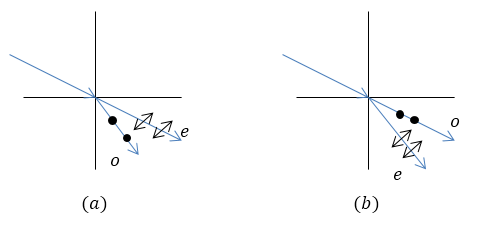
Рисунок 1.
Точки и стрелки на рис.1 указывают направление колебаний электрического вектора волны.
Предположим, что оптическая ось кристалла параллельна его поверхности. Если луч падает на поверхность кристалла перпендикулярно, то внутри кристалла возникают два луча (обыкновенный и необыкновенны), но они пространственно не разделяются. Когда лучи выходят из кристалла они имеют разность фаз и образуют поляризованную волну (эллиптически) в результате суперпозиции. В том случае, если на поверхность кристалла падает естественный свет, то выходя из кристалла, появляются эллиптически поляризованные волны с разными ориентациями эллипсов.
Пусть свет на вышеописанный кристалл падает под углом к поверхности. Результат двойного лучепреломления при этом зависит от угла между плоскостью падения и главной плоскостью.
Допустив, что плоскость падения луча нормальна оптической оси, получим: обыкновенный и необыкновенный лучи в плоскости падения, при этом показатели преломления обоих лучей не зависят от направления.
В случае если плоскость падения пересекает оптическую ось под углом не равным $90^circ$, картина двойного лучепреломления становится сложнее. Но при этом обыкновенный луч находится в плоскости падения, а необыкновенный выходит из нее. Для детализации картины следует строить пространственную модель на основе построения Гюйгенса.
Закон Малюса
При перпендикулярном падении луча на пластинку, которая вырезана из кристалла параллельно оптической оси, интенсивности колебаний в обыкновенном ($I_0$) и необыкновенном ($I_e$) лучах определяются из закона Малюса:
где $\beta $ -- угол между линией колебаний вектора $\overrightarrow{E}$ и оптической осью, $I$ -- интенсивность падающего луча. Из выражения (1) можно сделать вывод том, что вектор $\overrightarrow{E}$ падающей волны можно разложить на составляющие, которые параллельны и нормальны к оптической оси. Данные составляющие - есть векторы обыкновенной и необыкновенной волн света.
Поляризация при двойном лучепреломлении
Обыкновенный и необыкновенный лучи являются плоско поляризованными во взаимно перпендикулярных плоскостях. Значит, явление двойного лучепреломления можно использовать для получения поляризованного света. С этой целью обыкновенный и необыкновенный лучи разводят в пространстве и один из лучей уничтожают (поглощают).
Ели при выходе из кристаллической пластины один из лучей при выходе является плоско поляризованным, а другой сильно ослаблен, такая пластинка называется поляроидом. Поляроидом с хорошими свойствами является турмалин. При толщине в $1$мм пластинка из турмалина почти полностью поглощает обыкновенный луч. В необыкновенном луче при этом электрический вектор совершает колебания параллельно оптической оси.
Поляроид, используемый для получения поляризованного света, называют поляризатором. Его же при использовании для анализа поляризации света называют анализатором.
Через двоякопреломляющую призму пропускают свет. Показатель преломления обыкновенного луча при этом равен $n_0=1,658$, а необыкновенного луча $n_e=1,486.$ Угол призмы равен $\alpha =15.\ $ Под каким углом выйдет из призмы необыкновенный луч (${\theta '}_{pr(e)}$)?
Решение:
Совокупность кристаллов, которая дает поляризованный свет, называется поляризационной или двоякопреломляющей призмой. При этом поляризационной называют призму, если на выходе получается один поляризованный луч. В двоякопреломляющей призме на выходе оба луча.
Когда обыкновенный луч переходит границу между средами со взаимно перпендикулярными оптическими осями в первой среде луч становится необыкновенным во второй среде. И наоборот. Предельный угол преломления необыкновенного луча обозначим как: ${\theta }_{pr(e)}$, в таком случае запишем:
\[\frac{sin{\theta }_{pad(0)}}{sin ({\theta }_{pr\left(e\right)})}=\frac{n_e}{n_o}где $sin{\theta }_{pd(0)}=sin\propto $.Обозначим через ${\theta'}_{pr(e)}$ угол преломления луча при выходе из кристалла в воздух, запишем закон преломления в виде:
\[\frac{sin(\alpha -{\theta }_{pr(e)})}{sin{(\theta'}_{pr(e)})}=\frac{1}{n_e}\left(1.2\right),\]где угол падения на границу при выходе из вещества необыкновенного луча: $\alpha -{\theta }_{pr\left(e\right)}.$ Из уравнений (1.1) выразим $sin({\theta }_{pr\left(e\right)})$, имеем:
\[{sin \left({\theta }_{pr\left(e\right)}\right)\ }=\frac{sin\propto n_o}{n_e}\to {\theta }_{pr\left(e\right)}=arcsin(\frac{sin\propto n_o}{n_e})(1.3)\]Проведем вычисления:
\[{\theta }_{pr\left(e\right)}=arcsi{n \left(\frac{sin15{}^\circ \cdot 1,658}{1,486}\right)\ }=16,7847\]Из выражения (1.2) получим ${(\theta '}_{pr(e)}):$
\[{\theta'}_{pr(e)}=arcsin{\left(sin(\alpha-\theta_{pr(e)})n_e\right)\ }.\]Вычислим ${\theta'}_{pr(e)}$:
\[{\theta'}_{pr(e)}=arcsi{n \left(sin(15-16,7847)\cdot 1,486\right)=-2{}^\circ {14}'.\ }\]Ответ: ${\theta'}_{pr(e)}=2{}^\circ {14}'.$
Изобразите ход лучей при двойном лучепреломлении на поверхности отрицательного кристалла, если оптическая ось параллельна его поверхности, а плоскость падения луча совпадает с главной плоскостью.
Решение:
Как известно, при падении луча света под углом к поверхности кристалла особенности двойного лучепреломления зависят от угла между плоскостью падения и главной плоскостью. В условии задачи плоскость падения совпадает с главной плоскостью, то обыкновенный и необыкновенный лучи находятся в той же плоскости. Для отрицательного кристалла имеем рис. 2.
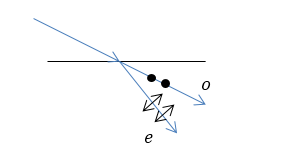
Рисунок 2.











