Допустим, что на пути распространения плоской волны света помещен непрозрачный экран с прямолинейным краем. Будем называть этот экран полуплоскостью, для того, чтобы не путать экран - преграду с экраном на котором рассматривают картину дифракции. Если свет распространяется прямолинейно, то на экране наблюдалась бы резкая тень от края полуплоскости. На самом деле в результате волнового характера света на экране возникает сложная картина дифракции. Расположение полуплоскости будем считать таким, что его плоскость совпадает с одной из волновых поверхностей. На некотором расстоянии $b$ за полуплоскостью поставим параллельный ей экран, на этом экране выберем точку $A$. Схема дифракции для заданного объекта изображена на рис.1. Линия, соединяющая источник света $S$ с точкой наблюдения $A$ проходит через точку $B$, расположенную на краю полубесконечной преграды. Эта линия перпендикулярна краю преграды. Линия края полубесконечности перпендикулярна плоскости рисунка.
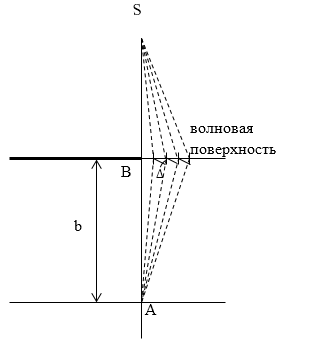
Рисунок 1.
При дифракции Френеля на полубесконечной непрозрачной плоскости с краем в виде прямой вторичные источники волн занимают полупространство. Соответственно, область интегрирования не является малой в сравнении с расстоянием до источника волн или до точки наблюдения. Не смотря на это, формальное использование принципа Гюйгенса Френеля для данного объекта ведет к результату, который согласуется с опытом.
Разобьем часть волновой поверхности, которая открыта на зоны, в виде узких прямых полосок, которые параллельны краю полуплоскости. Ширину зон примем такими, что отмерянные в плоскости рисунка расстояния от точки $A$ до краев любой зоны отличались на величину равную $\triangle .$ В таком случае колебания приходящие в точку $A$ от соседних зон отличны на постоянную величину.
Зоны, которые располагаются правее точки $A$ пронумеруем как: $1,2,3...$ Зоны левее точки $A$ будут иметь номера: $1',2',3'...$. Так, зоны имеющие номера $m\ и\ m'$ лежат симметрично относительно точки $A$ и имеют одинаковую ширину. Следовательно, колебания создаваемые вышеописанными зонами в точке $A$ совпадают по амплитуде и фазе.
Для установления зависимости амплитуды колебаний от номера зоны ($m$) следует оценить площади зон. В соответствии с рис.2 имеем, что суммарная ширина первых $m$ зон равна:
Так как зоны мы выбирали узкие ($\triangle \ll b$), то при не очень большом m величиной $m^2{\triangle }^2$ можно пренебречь, тогда имеем:
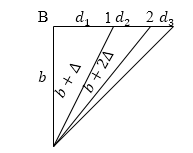
Рисунок 2.
Положим $m=1$, тогда из выражения (2) имеем:
Значит, выражение для суммы ширины первых $m$ зон запишем как:
Из выражения (4) получим:
Расчёты по формуле (5) дают соотношение:
В соответствии с выражением (6) находятся соотношение площадей зон.
Из формулы (6) можно сделать вывод о том, что для первых зон амплитуда убывает быстро, за тем убывание становится медленным. Если складывать колебания графически, то результирующая ломанная линия в начале идет более полого, чем для кольцевых зон (при равных площадях зон). Векторы, которые характеризуют вклад каждой подзоны, имеют одинаковую длину. Однако, разность фаз для соседних подзон не одинакова. Для первых зон в центральной части разность фаз близка к нулю, и растет при удалении от центра. Как результат векторная диаграмма имеет вид спирали, которую называют спиралью Корню.
Амплитуда в точке $A_0$, которая лежит напротив края экрана в два раза меньше, чем при отсутствии экрана. Интенсивность света в четыре раза меньше. Распределение интенсивностей на плоскости наблюдения, которая параллельна плоскости преграды, показана на рис. 3.
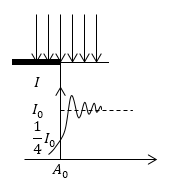
Рисунок 3.
Задание: Объясните, от чего зависит дифракционная картина на экране, если рассматривать дифракцию от прямолинейного края полуплоскости?
Решение:
Исходя из симметрии, можно сделать вывод о том, что дифракционная картина на демонстрационном экране будет зависеть только от расстояния до границы геометрической тени - точки $A$ (рис.1). Максимумы интенсивности света и минимумы (светлые и темные полосы) будут параллельны прямолинейному краю непрозрачной полуплоскости.
Задание: Что представляют собой зоны Шустера?
Решение:
В случае решения одномерных задач, например, рассматривая дифракцию на прямоугольной щели или краю экрана разбивать волновой фронт на кольцевые зоны не рационально. Удобнее разбить фронт волны на полосы, которые называют зонами Шустера. Пусть волновой фронт будет плоским (это не является принципиальным). Плоскость фронта волны ($AB$) перпендикулярна плоскости рисунка (рис.4). $P$ - точка наблюдения, $\left|OP\right|\bot \left|AB\right|$. Если провести цилиндрические коаксиальные поверхности с осями, проходящими через точку $Р$, перпендикулярными к плоскости рисунка. При этом радиусы цилиндров должны быть равны:
\[b,\ b+\frac{\lambda }{2},\ b+\frac{2\lambda }{2},\dots \left(2.1\right).\]В таком случае фронт волны разобьется зоны Шустера - прямоугольные полосы. Ширина последовательных зон Шустера равна:
\[d_1=\sqrt{b\lambda },\ d_2=\left(\sqrt{2}-1\right)\sqrt{b\lambda },d_3=\left(\sqrt{3}-\sqrt{2}\right)\sqrt{b\lambda },\dots \left(2.2\right).\]Зоны монотонно убывают. Как и в случае зон Френеля к зонам Шустера применяют графический метод.

Рисунок 4.











