Дифракция Фраунгофера на щели
Дифракция Фраунгофера на длинной, прямоугольной щели - простейший и важный с точки зрения применения на практике случай дифракции. Пусть ширина щели равна $b$, длина ее бесконечна. Плоская монохроматическая волна падает на щель перпендикулярно (рис.1).
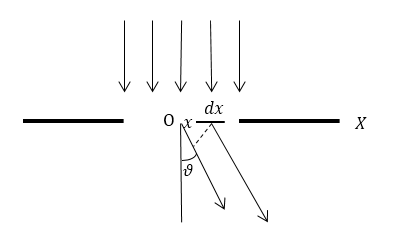
Рисунок 1.
Поле световой волны можно найти за щелью по принципу Гюйгенса как результат интерференции когерентных вторичных волн от разных точек волнового фронта щели. Рассмотрим вторичные волны, которые дает полоса волнового фронта, имеющая ширину $dx$ (эта полоса параллельна щели) (рис.1). Такие волны складываются в цилиндрическую волну Ее ось - выделенная полоса $dx.$ Угол $\vartheta$ (рис.1) считают малым, но следует учесть разность фаз волн, которые исходят между разными полосками (имеются в виду фазы колебаний на бесконечном расстоянии от щели). Волна, которая исходит от $dx$ опережает волну этого же направления, распространяющуюся из середины щели $O$ на величину: $kxsin\vartheta.$ Как результат, поле световой волны ($E$) на бесконечности, которое создается всей щелью, выразим как:
Интеграл (1) записан с точностью до множителей, которые не влияют на относительное распределение поля волны по направлениям. Из выражения (1) следует, что распределение интенсивности света в зависимости от направления имеет вид:
где $I_0$ - интенсивность в направлении падающей волны.
Функции $\frac{sin\alpha }{\alpha }\ и\ {\left(\frac{sin\alpha }{\alpha}\right)}^2$имеют максимум равный единице при $\alpha=0$. При $\alpha =m\pi,\ где\ m=\pm 1,\pm 2,\dots ,\ \frac{sin\alpha }{\alpha }={\left(\frac{sin\alpha }{\alpha }\right)}^2=0,\ $то есть имеется минимум интенсивности. Условие минимума можно записать как:
Выражение (3) значит, что разность хода волн крайних точек щели содержит цело число волн.
Между двумя соседними минимумами расположены максимумы разных порядков, чьи положения определены уравнением:
Можно считать, что максимумы лежат посередине между соседними минимумами.
Если свет падает на щель по углом ($\vartheta_0$), отличном от ${90}^0$, то условие дифракционного минимума перейдет в выражение:
В случае малых углов условие минимума можно записать как:
Основная доля света сосредотачивается в центральной полосе дифракции, то есть между минимумами первого и минус первого порядков.
Световые лучи, которые прошли через диафрагму, отклоняются от своего первоначального направления на угол:
где $D$ - поперечное сечение пучка (в таком направлении, где оно минимально). Данное изменение ширины пучка вызвано волновой природой света и не может быть ликвидировано при заданной ширине пучка. Следовательно, параллельные пучки света - идеализация.
В том случае, если ширина щели становится меньше (или порядка) длины волны, приближенный метод, использованный выше, становится неприменимым, задачу по поиску распределения поля следует решать, применяя уравнения Максвелла и соответствующие граничные условия.
Дифракция Фраунгофера на прямоугольном отверстии
Пусть свет падает перпендикулярно к плоскости экрана с отверстиями. Плоскость координат ($XY$) совместим с плоскостью экрана. Пусть $dF$ - элемент площади в плоскости экрана, его радиус вектор $\overrightarrow{r}(x,y)$. При этом направление световой волны после дифракции определим через единичный вектор $\overrightarrow{s}$. Разность хода между лучами, которые распространяются в направлении $\overrightarrow{s}$ из элемента $dF$ и начала координат ($O$) -- это длина отрезка $OA$, которая равна ($\overrightarrow{r}\overrightarrow{s}$) рис.2. Разность фаз при этом равна$\ k\left(\overrightarrow{r}\overrightarrow{s}\right).$ При этом поле для картины дифракции Фраунгофера представим как:
Если рассматривать прямоугольное отверстие, то применяют прямоугольную систему координат, выбирая оси координат параллельными сторонам отверстия.
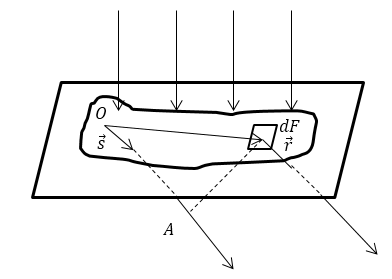
Рисунок 2.
Используя выражение (7) для прямоугольного отверстия со сторонами $a,b$, имеем:
где $\alpha =\frac{1}{2}kas_x=\frac{\pi as_x}{\lambda },\ \beta =\frac{1}{2}kas_y=\frac{\pi as_y}{\lambda }.$
Интенсивность определена в соответствии с формулой:
Дифракция Фраунгофера на круглом отверстии
Так как все оправы линз и объективов имеют в большинстве случаев круглую форму, то дифракция на круглом отверстии имеет большой практический интерес. В таком случае при вычислении интеграла (7) переходят к полярным координатам. Если углы дифракции малы, то интеграл выражается с помощью функции Бесселя первого порядка ($J_1(\alpha )$), где $\alpha =kR\vartheta =\frac{2\pi R\vartheta }{\lambda }$, где $R$ -радиус отверстия, $\vartheta$ - угол дифракции.
В центре картины дифракции находится круглый максимум, окруженный темными и светлыми кольцами дифракции. Максимумы интенсивности в светлых кольцах убывают. Радиус первого темного кольца находят из условия:
Угловой размер (${\theta }_0$) светлого круглого пятна, которое наблюдается из центра:
В пределах центрального светлого пятна сосредоточено $84\%$ всей энергии, которая проходит через отверстие.
Задание: Какое число длин волн размещается на ширине щели, если на нее нормально падает монохроматический свет? Направление распространения световой волны на четвертую темную полосу дифракции равно $2{}^\circ {12}'.$ Считайте щель узкой.
Решение:
В качестве основы для решения задачи используем условие минимумов для дифракции света, падающего перпендикулярно на узкую щель:
\[bsin\vartheta =m\lambda \left(1.1\right).\]Число длин волн размещается на ширине щели ($\frac{b}{\lambda }$) из выражения (1.1) равно:
\[\frac{b}{\lambda }=\frac{m}{sin\vartheta }\left(1.2\right).\]Из условия задачи имеем $m=4$, $\vartheta$=$2^\circ {12}'=2,2^\circ $.
Проведем вычисления:
\[\frac{b}{\lambda }=\frac{4}{sin2,2}=104.\]Ответ: $\frac{b}{\lambda }=104$.
Задание: На экран с круглым отверстием ($R=1,2$ мм) перпендикулярно падает параллельный пучок света с длиной волны равной $0,6$ мкм. Каково максимальное расстояние от отверстия до точки, расположенной на оси отверстия, где может наблюдаться самое темное пятно.
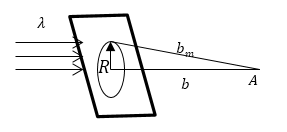
Рисунок 3.
Решение:
В качестве основы для решения задачи используем формулу для минимумов при дифракции на круглом отверстии:
\[R=\sqrt{bm\lambda \ }\to b=\frac{R^2}{m\lambda }\left(2.1\right)\ (где\ m-четное\ число).\]По условию задачи $m=2$ самый темный минимум. Переведем данные в систему СИ:
$R=1,2\ мм=1,2\cdot {10}^{-3}м$, $\lambda =0,6\ мкм=0,6\ \cdot {10}^{-6}м.$ Проведем вычисления:
\[b=\frac{{\left(1,2\cdot {10}^{-3}\right)}^2}{2\cdot 0,6\ \cdot {10}^{-6}}=1,2\ \left(м\right).\]Ответ: $b=1,2\ м$.












