
Рассмотрим ряд процессов, которые возникают в газе, если равновесие было нарушено. При этом сделаем следующие предположения: нарушения равновесия невелики, и если существует внешнее воздействие на систему, то неравновесное состояние может длиться бесконечно долго, оно не изменяется, процессы в таком газе будут стационарными.
Явления переноса обусловлены стремлением системы достигнуть равновесного состояния. Время, которое будет потрачено на достижение равновесного состояния, называется временем релаксации.
Нарушение равновесия в газе ведет к переносу из одних частей системы в другие вещества, энергии, заряда, импульса либо какой о другой величины. Интенсивность процесса переноса таковой является поток этой величины. Потоком физической величины называется количество этой величины, проходящей в единицу времени через некоторую воображаемую поверхность. Причем поверхность может иметь любую форму, быть замкнутой или незамкнутой. Поток величины -- скаляр, причем он считается положительным в зависимости от произвольного выбора.
Пусть G характеризует некоторое молекулярное свойство, отнесенное к одной молекуле. Это может быть энергия, импульс, концентрация и т.д. Если в равновесном состоянии G постоянно по объему, то при наличии градиента G имеется движение G в направлении его уменьшения. Пусть ось Ox направлена вдоль градиента G. Тогда полный поток $I_G$ в положительном направлении оси Ox в точке x имеет вид:
где $\left\langle \lambda \right\rangle$ - длина свободного пробега молекулы, $n_0$ концентрация частиц в веществе, $\left\langle v\right\rangle \ $- средняя скорость движения молекул.
Уравнение (1) является основным уравнением процессов переноса количества G.
Три вида процесса переноса
В молекулярной физике рассматривают три вида процесса переноса: диффузию, теплопроводность, вязкость.
В состоянии равновесия плотность каждой компоненты газа во всех точках системы одинакова. Перенос вещества (массы), который направлен на выравнивание концентрации газа, называют диффузией. Вообще говоря, диффузия может наблюдаться во всех состояниях вещества (и газах, и жидкостях, и твердых телах).
Пусть молекулы в некотором объеме газа распределены неравномерно. Неравновесную концентрацию обозначим $n_1(x)$. В уравнении (1) G -- характеристика переносимого вещества, следовательно, в нашем случае:
где $n_0$ -- равновесная концентрация. Тогда уравнение (1) примет вид:
где $D=\frac{1}{3}\left\langle v\right\rangle \left\langle \lambda \right\rangle $ -- коэффициент диффузии. Уравнение (3) называется уравнением Фика. При постоянной температуре коэффициент диффузии обратно пропорционален давлению:
По сути, закон Фика описывает процесс самодиффузии. Мы имеем дело с молекулами одного газа. Если имеется два и более сортов молекул, процесс диффузии значительно усложняется.
Уравнение Фурье
В состоянии термодинамического равновесия температура T во всех точках системы одинакова. Если температура в какой-то точке газа отличается температуры в другой точке системы, в системе возникает движение теплоты в таких направлениях, чтобы сделать температуру всех частей системы одинаковой. Связанный с этим движением перенос тепла называют теплопроводностью. В случае с теплопроводностью мы имеем дела с переносом энергии и G уравнения (1), в этом случае средняя энергия кинетической энергии молекулы:
где $i$- число степеней свободы молекулы, k-постоянная Больцмана, T -- термодинамическая температура, $R$ универсальная газовая постоянная, $c_{\mu V}$ молярная теплоемкость газа в изохорном процессе. При этом поток теплоты $I_q,\ $ если следовать уравнению (1) примет вид:
где $\chi =\frac{1}{3}n_0\left\langle v\right\rangle \left\langle \lambda \right\rangle \frac{c_{\mu V}}{N_A}=\frac{1}{3}n_0\cdot m\cdot \left\langle v\right\rangle \left\langle \lambda \right\rangle \frac{c_{\mu V}}{mN_A}=\frac{1}{3}\rho c_V\left\langle v\right\rangle \left\langle \lambda \right\rangle $,
$\rho $ -- плотность газа,
$c_V$ -- удельная теплоемкость газа при изохорном процессе,
$\chi $- коэффициент теплопроводности.
Уравнение (7) называется уравнением Фурье для теплопроводности (или законом Фурье). Теплопроводность не зависит от давления.
В равновесном состоянии разные части фазы газа покоятся друг относительно друга. При относительном движении фаз вещества друг относительно друга возникают силы трения или вязкость. Эти силы стремятся уменьшить скорость движения фаз. Явление вязкости объясняется тем, что в результате теплового движения молекулы газа перелетают из одного движущегося слоя в другой. Переносят свой импульс. В результате обмена импульсами молекулы, имеющие большую скорость тормозятся, а медленно движущееся молекулы, разгоняются. Соответственно выравнивается скорость движения слоев. Так, мы имеем дело с переносом импульса. В качестве G выступит выражение:
\[G=mv\ \left(8\right),\]где $v$- скорость движения слоя газа. В этом случае уравнение (1) принимает вид:
\[I_v=-\frac{1}{3}n_0\left\langle v\right\rangle \left\langle \lambda \right\rangle m\frac{\partial v}{\partial x}=-\eta \frac{\partial v}{\partial x}=\tau =\frac{F_{tr}}{\triangle S}(9),\]где $\eta =\frac{1}{3}n_0\left\langle v\right\rangle \left\langle \lambda \right\rangle m=\frac{1}{3}\rho \left\langle v\right\rangle \left\langle \lambda \right\rangle $, $\rho $ -- плотность газа, $\tau $ -- сила трения, действующая на единицу трущихся поверхностей слоев газа, $\eta $ -- динамическая вязкость. Выражение для динамической вязкости было получено Дж. Максвеллом. Динамическая вязкость не зависит от давления и $\eta \sim \sqrt{T},\ $ если не учитывать уменьшение поперечного сечения молекул с ростом температуры. Наряду с динамической вязкостью используют понятие кинематической вязкости $\nu $:
\[\nu =\frac{\eta }{\rho }(10).\]Задание: Идеальный газ находится в пространстве между двумя длинными коаксиальными цилиндрами$.\ $Средний радиус цилиндров R, $R_2-R_1=\triangle R$, причем $\Delta $R $
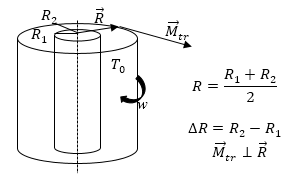
Рис. 1
Решение:
Выделим между имеющимися цилиндрами гипотетический цилиндрический слой газа радиуса R ($R_1 \[{\overrightarrow{M}}_{tr}=\left[\overrightarrow{F_{tr}}\overrightarrow{R}\right]\ \left(1.1\right).\]
Так как ${\overrightarrow{M}}_{tr}\bot \overrightarrow{R}$, то
\[M_{tr}=F_{tr}R\left(1.2\right).\]Из основного уравнения, для потока вязкости:
\[-\eta \frac{\partial v}{\partial x}=\frac{F_{tr}}{\triangle S}\ (1.3)\]Запишем модуль силы трения между слоями газа:
\[\left|F_{tr}\right|=\eta \frac{\partial v}{\partial x}\triangle S(1.4)\]Так как скорость вращения по условиям задачи небольшая, и зная площадь поверхность цилиндрического слоя (помним, что цилиндры длинные, площадями оснований пренебрегаем), запишем, что:
\[\left|F_{tr}\right|=\eta \frac{wR}{\triangle R}2\pi RL\ \left(1.5\right).\]Найдем момент сил трения из (1.2) и (1.5):
\[M_{tr}=\eta \frac{wR}{\triangle R}2\pi RLR=2\pi \eta \frac{wR^3}{\triangle R}L\ \ \left(1.6\right).\]Тогда момент сил трения, действующих на единицу длины внутреннего цилиндра равен:
\[{M_{tr}}'=\frac{M_{tr}}{L}=2\pi \eta \frac{w{R_1}^3}{\triangle R}\approx 2\pi \eta \frac{wR^3}{\triangle R}\ (1.7)\]Ответ: Момент сил трения, действующих на единицу длины внутреннего цилиндра равен $\approx 2\pi \eta \frac{wR^3}{\triangle R}$.
Задание: Пусть температура газа постоянна. Газ диффундирует. Как изменяется коэффициент диффузии с ростом давления?
Решение:
Запишем выражение, определяющее коэффициент диффузии:
\[D=\frac{1}{3}\left\langle v\right\rangle \left\langle \lambda \right\rangle \left(2.1\right)\]Средняя скорость молекул идеального газа определяется формулой:
\[\left\langle v\right\rangle =\sqrt{\frac{8RT}{\pi \mu }}\left(2.2\right).\]Из нее видно, что при постоянной температуре скорость постоянна.
\[\left\langle \lambda \right\rangle =\frac{1}{\sqrt{2}n\pi d^2}=\frac{kT}{\sqrt{2}p\pi d^2}\sim \frac{1}{p}\to D\sim \frac{1}{p}\ \left(2.3\right).\]Ответ: С ростом давления коэффициент диффузии уменьшается, при постоянной температуре обратно пропорционально давлению.











