Явление внутреннего трения
Явление внутреннего трения (вязкости) связано с возникновением сил трения между двумя слоями газа или жидкости, перемещающимися параллельно друг относительно друга с различными скоростями. Причиной вязкости является перенос молекулами импульса из одного слоя газа в другой (поперек направления движения слоев) (рис.1).
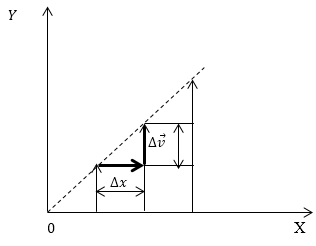
Рис. 1
В потоке газа молекулы участвуют в двух движениях одновременно: тепловом (хаотическом) со средней скоростью $\left\langle \overrightarrow{v}\right\rangle $ и упорядоченном со скоростью потока $\overrightarrow{v}$. Скорость теплового движения гораздо больше, чем скорость потока.
В результате теплового движения молекулы перелетают из одного слоя вещества в другой, переносят при этом свой импульс. В неподвижном газе средний импульс молекулы равен 0. Молекула в потоке газа обладает отличным от нуля импульсом. В результате обмена молекулами импульс упорядоченного движения быстрее движущегося слоя уменьшается, а другого наоборот. Слой вещества, который движется быстрее, тормозится, а медленный ускоряется. Уравнение Ньютона для вязкости в одномерном случае $(v=v(x))$:
$dF$- сила внутреннего трения, действующая на площадку dS поверхностного слоя, $\frac{dv}{dx}$- проекция градиента скорости движения слоев на направление оси Ox, в направлении перпендикулярном к поверхности слоя, $\eta $- коэффициент вязкости. Сила трения $F_{\tau }$, отнесенная к площади трущихся поверхностей равна потоку импульса упорядоченного движения частиц в перпендикулярном направлении к скорости. Используем основное уравнение для явлений переноса. В нашем случае $G=mv$, следовательно:
где $\eta =\frac{1}{3}n_0\left\langle v\right\rangle \left\langle \lambda \right\rangle m=\frac{1}{3}\rho \left\langle v\right\rangle \left\langle \lambda \right\rangle $ -- динамическая вязкость, $\rho =n_0m$ -- плотность газа. Знак $F_{\tau }$ учитывает, что сила трения, действующая на более быстрые слои, направлена против скорости. Динамическая вязкость не зависит от давления и растет, в основном, пропорционально $\sqrt{T}$. Более точные теоретические расчеты приводят к замене множителя $\frac{1}{3}$ на коэффициент, который зависит от характера взаимодействия молекул. Для молекул, сталкивающихся, как гладкие шары, он равен 0,499. Вообще этот коэффициент зависит о температуры.
Кинематическая вязкость
Наряду с динамической вязкостью используют и кинематическую вязкость:
Согласно кинетической теории газов между коэффициентами переноса существует связь:
где $c_V$- удельная теплоемкость газа при изохорном процессе. На практике используется более точное соотношение коэффициентов переноса:
где $\alpha $- множитель, зависящий от числа степеней свободы молекулы газа. Так для одноатомной молекулы газа $\alpha =2,5$, двухатомного $\alpha =1,9$, трехатомного $\alpha =1,5-1,75.$
Задание: Определить коэффициент вязкости газа с молярной массой $\mu $ при температуре T. Эффективный диаметр молекулы газа принять равным d.
Решение:
Запишем формулу для определения коэффициента вязкости:
\[\eta =\frac{1}{3}\rho \left\langle v\right\rangle \left\langle \lambda \right\rangle \ \left(1.1\right).\]Плотность газа определим из уравнения Менделеева -- Клайперона:
\[pV=\frac{m}{\mu }RT\to \rho =\frac{m}{V}=\frac{p\mu }{RT}\left(1.2\right)\] \[\left\langle v\right\rangle =\sqrt{\frac{8RT}{\pi \mu }}\left(1.2\right)\] \[\left\langle \lambda \right\rangle =\frac{1}{\sqrt{2}\pi d^2n},\ p=nkT\to \left\langle \lambda \right\rangle =\frac{kT}{\sqrt{2}\pi d^2p}\left(1.3\right)\]Подставим (1.2), (1.3) в (1.1), получим:
\[\eta =\frac{1}{3}\frac{p\mu }{RT}\sqrt{\frac{8RT}{\pi \mu }}\frac{kT}{\sqrt{2}\pi d^2p}=\frac{1}{{3\pi N}_Ad^2}\sqrt{4RT\mu }\]Ответ: Вязкости газа заданных параметров $\eta =\frac{1}{{3\pi N}_Ad^2}\sqrt{4RT\mu }$.
Задание: Газ заполняет пространство между двумя длинными коаксиальными цилиндрами, радиусы которых R1 и R2, причем R1$
Решение:
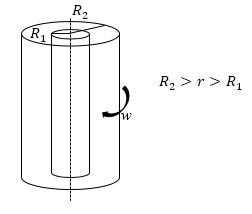
Рис. 2
По определению момента сил $M_{tr}$ вращающегося тела запишем:
\[M_{tr}=F_{tr}r\ \left(2.1\right)\]C другой стороны при длине цилиндра равной l по условию задачи:
\[M_{tr}=N_1\cdot l\ (2.2),\ \]Кроме того из условия задачи имеем:
\[F_{tr}=\sigma \triangle S\ =\ \eta \cdot r\ \frac{d\omega }{dr}2\pi rl=2\eta \pi r^2l\frac{d\omega }{dr}\ \left(2.3\right)\]Тогда
\[M_{tr}=2\eta \pi r^3l\frac{d\omega }{dr}=N_1\cdot l\to 2\eta \pi r^3\frac{d\omega }{dr}=N_1(2.4)\]Разделим переменные в уравнении (2.4), получим:
\[\eta d\omega =\frac{N_1}{2\pi }\frac{dr}{r^3}\ \left(2.5\right)\]Проинтегрируем обе части уравнения по соответствующим переменным:
\[\eta \int\nolimits^{w_c}_0{d\omega }=\frac{N_1}{2\pi }\int\nolimits^{R_2}_{R_1}{\frac{dr}{r^3}}\ \left(2.6\right)\] \[\eta w_c=\frac{N_1}{4\pi }\left(\frac{1}{{R_1}^2}-\frac{1}{{R_2}^2}\right)\to \eta =\frac{N_1}{4\pi w_c}\left(\frac{1}{{R_1}^2}-\frac{1}{{R_2}^2}\right)\]Ответ: Коэффициент вязкости газа будет $\eta =\frac{N_1}{4\pi w_c}\left(\frac{1}{{R_1}^2}-\frac{1}{{R_2}^2}\right).$











