Параметрами газа называют (параметры состояния) совокупность физических величин, которые определяют макроскопические свойства системы (плотность $\rho ,$ энергия E, температура T, давление p и т.д.).
Параметры состояния не всегда имеют определенные значения. К примеру, подогреваемое с одной стороны и охлаждаемое с другой стороны тело имеет различную температуру в разных точках этого тела. Параметры газа связаны между собой. Поэтому однозначное определение состояния системы возможно с помощью ограниченного количества значений параметров. Основными параметрами состояния являются: давление, температура, удельный (или молярный) объем $V_{\mu }$.
Что такое внешние параметры
Существуют внешние и внутренние параметры состояния газа.
Внешними параметрами состояния называют параметры, которые зависят только от обобщенных координат внешних тел, с которыми взаимодействует система.
Пример внешнего параметра для газа является объем, который зависит от стенок сосуда.
Внутренними параметрами состояния газа являются параметры, которые определяются не только обобщёнными координатами, внешних тел, но и усредненными значениями координат и скоростей частиц входящих в систему.
К внутренним параметрам, можно отнести температуру.
Что такое давление
Давлением $(p)\ $называют физическую величину, равную:
\[p={\mathop{lim}_{\triangle S\to 0} \frac{\triangle F_n}{\triangle S}=\frac{dF_n}{dS},\ \left(1\right)\ }\]где $F_n$ -- проекция силы на нормаль к участку тела $\triangle S$, $\triangle S$- площадь тела. Давление газа создается в результате многочисленных ударов молекул о стенки сосуда, в котором он находится. Очевидно, что давление зависит от скорости движения молекул газа, их массы и количества.
Единица измерения давления в системе СИ паскаль -- $\frac{H}{м^2}$=Па. К альтернативным единицам измерения давления относят -- техническую атмосферу, которая равна $1 атм=1 кгс/см^2$. Также для измерения давления применяют высоту столба жидкости (воды, ртути, спирта) в капилляре, если давление небольшое. При этом давление рассчитывается по формуле:
\[p=\rho \cdot g\cdot h\ \left(2\right),\]где $\rho $- плотность вещества (жидкости) в $кг/м^3$, $g=9,80665(м/c^2)$- ускорение свободного падения, соответственно:
\[h=\frac{p}{\rho \cdot g}\left(3\right).\]В таком случае считают, что давление измеряется в м вод. ст. (метр водяного столба) или мм.рт.ст (миллиметр ртутного столба).
Давление иногда разделяют на: атмосферное, избыточное и давление в вакууме (т.е. ниже атмосферного).
Удельным объемом $V_u$ называют величину, обратную плотности $\rho :\ $
\[V_u=\frac{1}{\rho }\left(4\right).\]Для однородного тела удельный объем:
\[V_u=\frac{V}{m}(5).\]В системе СИ за единицу количества вещества принят моль. Количество одинаковых частиц, содержащихся в одном моле, называют постоянной (числом) Авогадро $N_A=6,022\cdot {10}^{23} моль^{-1}$.
Молярная масса и молярный объем
Молярной массой химически однородного вещества называют величину:
\[\mu =\frac{m}{\nu }(6),\]где m -- масса, $\nu $ -- число молей вещества. Молярным объемом называют величину:
\[V_{\mu }=\mu V_u=\frac{\mu }{\rho }\left(7\right).\]Иногда вместо массы газа рассматривают число его молекул (N) в заданном объеме:
\[N=N_A\frac{m}{\mu }\left(8\right).\]Температурой (t, или T) называют физическую величину, характеризующую степень нагретости тела. Различают несколько видов температуры (в зависимости от используемой шкалы измерения).
Внутренние параметры газа, который находится в равновесном состоянии, зависят только от ее внешних параметров и температуры:
\[y_k=f\left(x_{1,},x_{2,},\dots ,\ x_n,\ T\right)\left(9\right),\]где $y_k$- внутренний параметр, $x_{1,},x_{2,},\dots ,\ x_n$- внешние параметры.
К примеру, равновесное состояние физически однородной термодинамической системы полностью определяется двумя параметрами. Поэтому состояние системы можно охарактеризовать уравнением:
\[p=f_0\left(V,T\right)\left(10\right).\]Очень часто в условиях задачи записано, газ находится в нормальных условиях, это значит, что давление равно $1\ амтм\approx 10^5Па$, температура $t=0^oC$.
К основным параметрам газа так же относят внутреннюю энергию U газа. Для газа, на который не действуют внешние силы, находящийся в состоянии макроскопического равновесия внутренняя энергия представляет собой полную энергию системы. Внутренняя энергия включает в себя энергию теплового (хаотического) движения частиц и энергию их взаимодействия. Она однозначно определяет состояние газа как системы. Изменение внутренней энергии не зависит от способа перехода системы из одного состояния в другое, а зависит только от конечного и начального состояния газа (т.е.U - функция состояния):
\[\triangle U=U_2-U_{1\ }(11)\]Внутренняя энергия газа является аддитивной, то есть полная внутренняя энергия системы есть сумма внутренних энергий ее макрочастей. При невысоких температурах часто внутреннюю энергию идеального газа принимают равной суммарной кинетической энергии его молекул. Внутренняя энергия идеального газа зависит от термодинамической температуры T газа:
\[U=\int\nolimits^T_0{C_VdT}+U_0=m\left(\int\nolimits^T_0{c_VdT}+u_0\right)\left(12\right),\]где $C_V$- теплоемкость газа при изохорном процессе, $c_V=\frac{C_V}{m}$ -- удельная теплоемкость, $U_0$- внутренняя энергия газа при T=0K, $u_0=\frac{U_0}{m}.$ Довольно часто $U_0$ полагают равной 0.
Еще один параметр газа, как термодинамической системы -- энтальпия H (теплосодержание, тепловая функция). Н как и внутренняя энергия является функцией состояния. По определению:
\[H=U+pV\left(13\right).\]Для одноатомных газов:
\[H=C_pT+H_{0\ }\left(14\right),\]где $C_p$ -- теплоемкость газа при изобарном процессе, $H_{0\ }=U_0$- энтальпия газа при T=0K.
Энтальпия смеси идеальных газов равна сумме энтальпий компонентов.
Следующий параметр газа и функция состояния -- энтропия (S). Для обратимого процесса:
\[S=\int\nolimits^T_0{\frac{\delta Q}{T}}+S_0\left(15\right),\]где $S_0=const$, $\delta Q$- элементарное количество тепла, переданное газу. Адиабатный процесс является изоэнтропийным. Знак изменения энтропии газа показывает направление теплообмена. При нагревании газа dS$ > $0, при охлаждении dS$ \[S\left(V,T\right)=\int\nolimits^T_0{C_V\frac{dT}{T}}+{S'}_0(16)\]
либо
\[S\left(p,T\right)=\int\nolimits^T_0{C_p\frac{dT}{T}}+{S^{''}}_0\left(17\right),\]где $\int\nolimits^T_0{C_V\frac{dT}{T}}$ для изохорного процесса, $\int\nolimits^T_0{C_p\frac{dT}{T}}$ -- изобарного процесса. Процессы обратимы!
${S'}_0=S\left(V,0\right)\ и\ {S^{''}}_0=S\left(p,0\right).$ Энтропия смеси равна сумме энтропий компонент.
Задание: На графике в осях p(V) изображены обратимые процессы, производимые в идеальном газе. Сравните изменения энтропий идеального газа для процесса 1a2 ($\triangle S_{1a2})$ и процесса 1b2 ($\triangle S_{1b2})$.
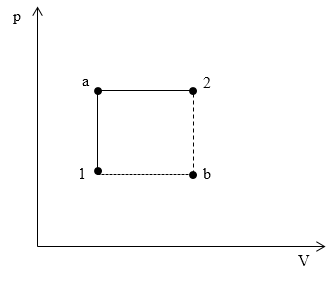
Рис. 1
Решение:
Энтропия является функцией состояния для идеального газа. Это значит, что ее изменение не зависит от способа перехода из одного состояния в другое, а зависит только от начального и конечного состояний. Поэтому $\triangle S_{1a2}$=$\triangle S_{1b2}$.
Ответ: $\triangle S_{1a2}$=$\triangle S_{1b2}$.
Задание: Найти изменение энтропии идеального газа в адиабатном процессе, в изобарном процессе.
Решение:
Запишем определение изменения энтропии для обратимого процесса:
\[\triangle S=\int\nolimits^{T_2}_{T_1}{\frac{\delta Q}{T}}\left(2.1\right)\]Адиабатный процесс -- это процесс, который происходит без подведения системе (газу) тепла, соответственно: $\delta Q=0\to \triangle S=0.\ $Энтропия в адиабатном процессе не изменяется.
Для изобарного процесса $p=const.$ $\delta Q=dU+dA$ по первому началу термодинамики, где $dU=\frac{i}{2}\nu RdT$, $dA=pdV$. Подставим $dU\ и\ dA$ в (2.1):
\[\triangle S=\int\nolimits^{T_2}_{T_1}{\frac{\frac{i}{2}\nu RdT}{T}}+\int\nolimits^{T_2}_{T_1}{\frac{pdV}{T}}=\frac{i}{2}\nu Rln\frac{T_2}{T_1}+\int\nolimits^{T_2}_{T_1}{\frac{\nu RdT}{T}}=\frac{i}{2}\nu Rln\frac{T_2}{T_1}+\nu Rln\frac{T_2}{T_1}=\nu Rln\frac{T_2}{T_1}\left(\frac{i+2}{2}\right).\]Из уравнения Менделеева--Клайперона:
\[pV=\nu RT,\ при\ p=const,\ \to pdV=\nu RdT\]Ответ: Изменение энтропии идеального газа в адиабатном процессе равно 0. Изменение энтропии идеального газа в изобарном процессе $\triangle S=\left(\frac{i+2}{2}\right)\nu Rln\frac{T_2}{T_1}=с_{\mu p}\nu ln\frac{T_2}{T_1}$, где $с_{\mu p}$- молярная теплоемкость идеального газа в изобарном процессе.











