Волны де Бройля - волны вероятности, которые определяют плотность вероятности обнаружения объекта в заданной точке конфигурационного пространства.
Формула для определения длины волны записывается следующим образом:
Корпускулярно - волновая природа материи является одним из основных аспектов квантовой механики: каждый материальный объект может проявлять волновые свойства, а это значит, что он может обладать свойствами дифракции и интерференции.
В связи с тем, что длина волны электронов и материи чрезвычайно мала по сравнению с длиной волны света, электроны подходят для наблюдения за мелкими объектами. Это было использовано, в частности, для построения электронного микроскопа, который имеет разрешение во много раз выше, чем оптический микроскоп.
Эти соображения относятся к свободному движению частиц (которые соответствуют плоским волнам).
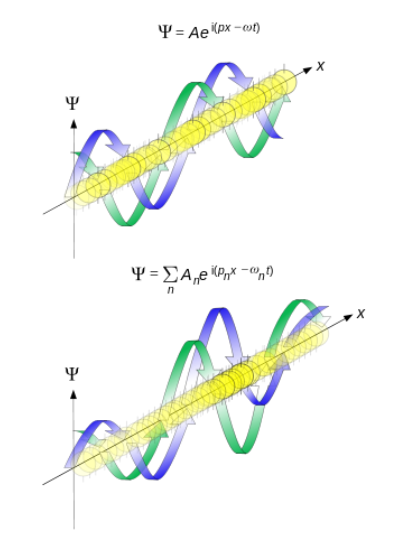
Рисунок 1. Распространение Волн Де Бройля
Пример для макроскопического объекта
Макроскопические объекты можно рассматривать как волны де Бройля, а длина волны настолько мала, что она становится неизмерима. Говорят, что макроскопические объекты не раскрывают их собственной волны. Например, можно рассчитать, что для человека $50$ - кг, движущегося со скоростью $10$ км/ч длина волны равна
Это значение настолько мало, что невозможно обнаружить волновые свойства человека.
Гипотеза де Бройля
Де Бройль, в $1924$ году, защищая кандидатскую диссертацию, предположил, что, свет имеет как волнообразные и частицеподобные свойства, так и электроны имеют волновые свойства.
где $\lambda $ - длина волны фотона.
Таким образом, де Бройль предложил ввести отношение между импульсом и длиной волны фотона, так что длина волны была выражена импульсом частицы.
Эта гипотеза не имела экспериментальной базы и была чисто теоретическим предположением.
Но в дальнейшем эти результаты были подтверждены Джорджом Томсоном в Шотландии, за которую в $1937$ году он получил Нобелевскую премию по физике.
Фазовая скорость
В квантовой механике, частицы ведут себя как волны с комплексными фазами. Фазовая скорость равна произведению частоты, умноженной на длину волны.
Используя релятивистские соотношения для энергии и импульса, мы имеем
где${\rm \ E}$ является полной энергией частицы, ${\rm p}$ импульс, $\gamma $ фактор Лоренца.
Групповая скорость
Альберт Эйнштейн впервые объяснил корпускулярно - волновой дуализм света в $1905$ году.
И в релятивистской и нерелятивистской квантовой физике, мы можем определить групповую скорость частицы волновой функцией со скоростью частицы. Квантовая механика очень четко продемонстрировала эту гипотезу, и отношение было показано для частиц такого размера, как молекулы.
где${\rm \ E}$ является полной энергией частицы, ${\rm p}$ импульс, $h$ является постоянной Планка.
Электрон обладает кинетической энергией $T=1,02$ МэВ. Во сколько раз изменится длина волны де Бройля, если кинетическая энергия $T$ электрона уменьшится вдвое?
Решение:
Связь длины волны де Бройля с кинетической энергией $E_к$ в классическом приближении
\[\lambda =\frac{h}{\sqrt{2\cdot m\cdot E_к}}\]В релятивистском случае длину волны нужно вычислять по формуле
\[\lambda =\frac{h\cdot c}{\sqrt{\left(E_к\left(E_к+2m_ec^2\right)\right)}}\]Где $m_ec^2-$ масса покоя электрона и равна $0,511$ МэВ.
В нашем случае кинетическая энергия $E_к$ сравнима с массой покоя электрона и поэтому нужно использовать формулу для релятивистского случая.
Тогда
\[\lambda =\frac{h\cdot c}{\sqrt{\left(E_к\left(E_к+2m_ec^2\right)\right)}}\]И
\[{\lambda }^,=\frac{h\cdot c}{\sqrt{\left({E^,}_к\left({E^,}_к+2m_ec^2\right)\right)}}=\lambda =\frac{h\cdot c}{\sqrt{\left({0,5E}_к\left(0,5E_к+2m_ec^2\right)\right)}}\]Поэтому искомая величина равна
\[\frac{{\lambda }^,}{\lambda }=\frac{\sqrt{\left(E_к\left(E_к+2m_ec^2\right)\right)}}{\sqrt{\left({0,5E}_к\left(0,5E_к+2m_ec^2\right)\right)}}=\sqrt{\frac{\left(E_к+2m_ec^2\right)}{0,5\cdot \left(0,5E_к+2m_ec^2\right)}}\]Подставляем числа (переводя одновременно все величины в систему СИ).
\[\frac{{\lambda }^,}{\lambda }=\sqrt{\frac{\left(1,02\ МэВ+2\cdot 0,51\ МэВ\right)}{0,5\cdot \left(0,5\cdot 1,02\ МэВ+2\cdot 0,51\ МэВ\right)}}=1,63\]Ответ: длина волны де Бройля увеличится в $1,63$ раз.












