Необходимость введения тензора магнитной проницаемости
Материальное уравнение для магнитного поля, можно записать как:
где системе СИ ${\mu }_0=4\pi \cdot 10^{-7}$ -- магнитная постоянная, $\mu $- магнитная проницаемость вещества. Из опыта получено, что в слабых полях для изотропных сред $\mu $ -- величина постоянная и определяется магнитными свойствами вещества и в таком случае вектор магнитной индукции совпадает по направлению с вектором напряженности магнитного поля. В анизотропных средах направления векторов $\overrightarrow{B}$ и $\overrightarrow{H}$ не совпадают. Связь между ними осуществляется тензором магнитной проницаемости.
Запись тензора магнитной индукции
Рассмотрим анизотропную среду, что означает, вектор магнитной индукции ($\overrightarrow{B}$) не будет параллелен вектору напряженности магнитного поля ($\overrightarrow{H}$). Представим вектор магнитной индукции в виде:
а вектор напряженности магнитного поля как:
где $\overrightarrow{e_i},\ \overrightarrow{e_j}$ -- единичные векторы.
В этом случае, связь (1) запишем в виде:
или, тоже самое, но более компактно:
где индексы i,j -- нумеруют компоненты по осям декартовой системы координат ($i=x,\ y,z;j=x,\ y,z.\ )$), ${\mu }_{ij}$ -- тензор магнитной проницаемости вещества. Девять величин ${\mu }_{xx},\ {\mu }_{xy},{\mu }_{xz},\dots ,$ - являются постоянными среды и составляют тензор магнитной проницаемости. Соответственно, вектор магнитной индукции ($\overrightarrow{B}$) равен произведению тензора магнитной проницаемости на вектор напряженности электрического поля ($\overrightarrow{H}$). При формальной тензорной записи знак суммы опускают, суммирование обозначают двукратным повторением индекса (в нашем случае индекс j), то есть:
Свойство симметрии тензора магнитной проницаемости
Тензор магнитной проницаемости симметричен при любом значении поля, то есть можно записать следующее:
Главные значения ${\mu }_i$ называют главными коэффициентами магнитной проницаемости. Если ${\mu }_i > 1,$ то кристалл парамагнитен в соответствующем главном направлении, если ${\mu }_i
Симметрия тензора ${\mu }_{ij}$- необходимое и достаточное условие для выполнения закона сохранения энергии. Из девяти компонент тензора магнитной проницаемости только шесть независимы. Симметричность рассматриваемого нами тензора позволяет привести выражение для плотности энергии магнитного поля к такой форме, при которой сохраняются только квадраты компонент поля и отсутствуют их произведения. В такой системе (а она называется системой главных осей) материальные уравнения магнитного поля имеют вид:
Выражение для плотности энергии магнитного поля для рассматриваемого нами случая будет иметь вид:
где величины ${\mu }_x,{\mu }_y,{\mu }_z$ -- называются главными магнитными проницаемостями. Из приведенных выше формул следует, что векторы $\overrightarrow{В}$ и $\overrightarrow{H}$ всегда имеют разные направления, если направление вектора напряженности поля не совпадает с одной из главных осей или все главные магнитные проницаемости не равны друг другу.
Связь тензоров магнитной восприимчивости и магнитной проницаемости
Связь тензоров магнитной проницаемости и магнитной восприимчивости имеет вид:
где ${\delta }_{ij}-\ $единичный тензор, который равен:
При этом связь между векторами напряжённости и намагниченности ($\overrightarrow{J}$) описывается уравнением, которое включает симметричный тензор магнитной восприимчивости ${\varkappa }_{ki}:$
Задание: Докажите, что тензор магнитной проницаемости симметричен. Считать, что поглощение отсутствует, электрическое поле однородно и изотропно.
Решение:
В качестве основы для доказательства используем выражения для плотности энергии электрического ($w_e$) и магнитного полей ($w_m$):
\[w_e=\frac{{\varepsilon }_0}{2}\varepsilon E^2\left(1.1\right).\] \[w_m=\frac{{\mu }_0}{2}{\mu }_{ij}H_iH_j\left(1.2\right).\]где $H_iH_j$- компоненты вектора напряжённости магнитного поля.
Выражение для вектора Умова -- Пойнтинга ($\overrightarrow{S}$):
\[\overrightarrow{S}=\left[\overrightarrow{E}\times \overrightarrow{H}\right]\left(1.3\right).\]Первое и второе уравнения из системы уравнений Максвелла:
\[rot\overrightarrow{E}=-\frac{\partial \overrightarrow{B}}{\partial t}\ \left(1.4\right),\] \[rot\overrightarrow{H}=\overrightarrow{j}+\frac{\partial \overrightarrow{D}}{\partial t}\ \left(1.5\right),\]Уравнение (1.5) системы умножим на вектор напряженности электрического поля ($\overrightarrow{E}$), уравнение (1.4) умножим на вектор напряженности магнитного поля ($\overrightarrow{H}$), сложим два полученных выражения при этом опустим ток проводимости, получим:
\[\overrightarrow{E}rot\overrightarrow{H}-\overrightarrow{H}rot\overrightarrow{E}=\overrightarrow{j}\cdot \overrightarrow{E}+\overrightarrow{E}\cdot \frac{\partial \overrightarrow{D}}{\partial t}+\overrightarrow{H}\cdot \frac{\partial \overrightarrow{B}}{\partial t}\ (1.6)\] \[-div\overrightarrow{S}=-div\left[\overrightarrow{E}\times \overrightarrow{H}\right]=\overrightarrow{E}\cdot \dot{\overrightarrow{D}}+\overrightarrow{B}\cdot \dot{\overrightarrow{H}}={\mu }_0H_i{\mu }_{ij}\dot{H_j}+\frac{1}{2}{\varepsilon }_0\frac{d}{dt}\left(\varepsilon E^2\right)\left(1.7\right),\]При преобразовании дивергенции векторного произведения мы использовали известное векторное равенство:
\[div\left[\overrightarrow{E}\times \overrightarrow{H}\right]=\overrightarrow{H}rot\overrightarrow{E}-\overrightarrow{E}rot\overrightarrow{H}\ \left(1.8\right).\]Исходя из уравнения (1.2) мы получили, что в уравнении (1.7) вторым слагаемым является:
\[\frac{1}{2}{\varepsilon }_0\frac{d}{dt}\left(\varepsilon E^2\right)=\frac{d}{dt}\left(w_e\right)\left(1.9\right).\]Так как мы условились, что среда является однородной и изотропной для электрического поля, то такая производная равна нулю. Изучим производную по времени от плотности энергии магнитного поля:
\[\frac{d}{dt}w_m=\frac{{\mu }_0}{2}{\frac{d}{dt}(\mu }_{ij}H_iH_j)=\frac{{\mu }_0}{2}{\mu }_{ij}\left(\dot{H_i}H_j+H_i\dot{H_j}\right)\left(1.10\right).\]Выражение ${\mu }_0\sum\limits_{i,j}{H_i{\mu }_{ij}\dot{H_j}}$ будет представлять собой скорость изменения плотности энергии магнитного поля только если:
\[{\mu }_0H_i{\mu }_{ij}\dot{H_j}=\frac{d}{dt}w_m=\frac{{\mu }_0}{2}{\mu }_{ij}\left(\dot{H_i}H_j+H_i\dot{H_j}\right)\ \left(1.11\right),\]то есть при:
\[{\mu }_{ij}\left(\dot{H_i}H_j-H_i\dot{H_j}\right)=0\ \left(1.12\right).\]Мы понимаем, что изменение индексов в выражении (1.12) фиктивно, так как они принимают одни и те же значения (x,y,z). Из уравнения (1.12) следует, что:
\[{\mu }_{ij}={\mu }_{ji}.\]Что требовалось доказать.
Задание: Покажите, используя тензор магнитной проницаемости, что векторы $\overrightarrow{B}\ $и $\overrightarrow{H}$ не коллинеарны в неизотопной среде.
Решение:
Анизотропная среда характеризуется тензором магнитной проницаемости второго ранга:
\[{\mu }_{ij}=\left| \begin{array}{ccc} {\mu }_{xx} & {\mu }_{xy} & {\mu }_{xz} \\ {\mu }_{yx} & {\mu }_{yy} & {\mu }_{yz} \\ {\mu }_{zx} & {\mu }_{zy} & {\mu }_{zz} \end{array} \right|\left(2.1\right).\]Это означает, что каждая составляющая вектора $\overrightarrow{В}$ выражается через все три составляющие вектора напряженности магнитного поля:
\[\left\{ \begin{array}{c} B_x={\mu }_0\left({\mu }_{xx}H_x+{\mu }_{xy}H_y+{\mu }_{xz}H_z\right), \\ B_y={\mu }_0\left({\mu }_{yx}H_x+{\mu }_{yy}H_y+{\mu }_{yz}H_z\right) \\ B_z={\mu }_0\left({\mu }_{zx}H_x+{\mu }_{zy}H_y+{\mu }_{zz}H_z\right). \end{array} \right.,\left(2.2\right).\]Выберем главные оси X,Y,Z и зафиксируем их по отношению к веществу. В таком случаем можно записать:
\[\left\{ \begin{array}{c} B_x={{\mu }_0\mu }_xH_x, \\ B_y={{\mu }_0\mu }_yH_y \\ B_z={\mu }_0{\mu }_zH_z. \end{array} ,\right.\ \left(2.3\right).\]Система (2.3) означает, что тензор магнитной проницаемости приведен к виду:
\[{\mu }_{ij}=\left| \begin{array}{ccc} {\mu }_x & 0 & 0 \\ 0 & {\mu }_y & 0 \\ 0 & 0 & {\mu }_z \end{array} \right|(2.2)\]С точки зрения математики -- это диагонализация матрицы (2.1). Если ${\mu }_x\ne {\mu }_y\ne {\mu }_z$, то при умножении составляющих вектора $\overrightarrow{H}$ на соответствующие компоненты тензора магнитной проницаемости, компоненты вектора магнитной индукции (2.3) не совпадут по направлению с вектором $\overrightarrow{H}$. (рис.1).
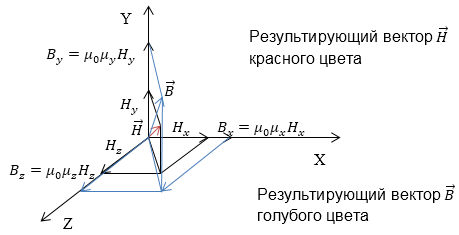
Рис. 1











