При рассмотрении движения тела с ускорением особого внимания заслуживает движение тела с ускорением, постоянным по величине и направлению. Такое движение по определению является поступательным - поскольку вектор скорости, как и вектор ускорения, имеет постоянное направление, и траектория тела является прямой линией.
Движение тела с ускорением, постоянным по величине и направлению, называют равнопеременным движением, и подразделяют его на равноускоренное -- когда $\overrightarrow{a}>0$, и равнозамедленное -- когда $\overrightarrow{a}
При равноускоренном движении мгновенное ускорение равно среднему ускорению: $\overrightarrow{\ a}=\left\langle \overrightarrow{а}\right\rangle =\frac{\triangle v}{\triangle t}=const$, где $\triangle \overrightarrow{v}=\overrightarrow{v}-{\overrightarrow{v}}_0$ -- приращение скорости за время $\triangle t=t-t_0$, ${\overrightarrow{v}}_0=\overrightarrow{v}\left(t_0\right)$ -- начальная скорость, $t_0$ -- начальный момент времени.
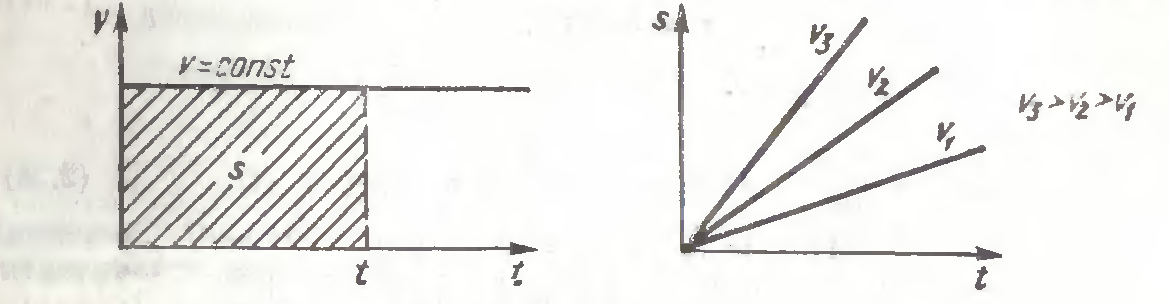
Рисунок 1. График скорости при равноускоренном движении
Скорость равноускоренного движения $\overrightarrow{v}\left(t\right)$ в момент времени t определяется из соотношения
где $a_x,\ a_y,a_z$ --- проекции вектора $\overrightarrow{a}$ на оси координат.
Уравнение для траектории движения $\overrightarrow{r}\left(t\right)$ имеет вид:
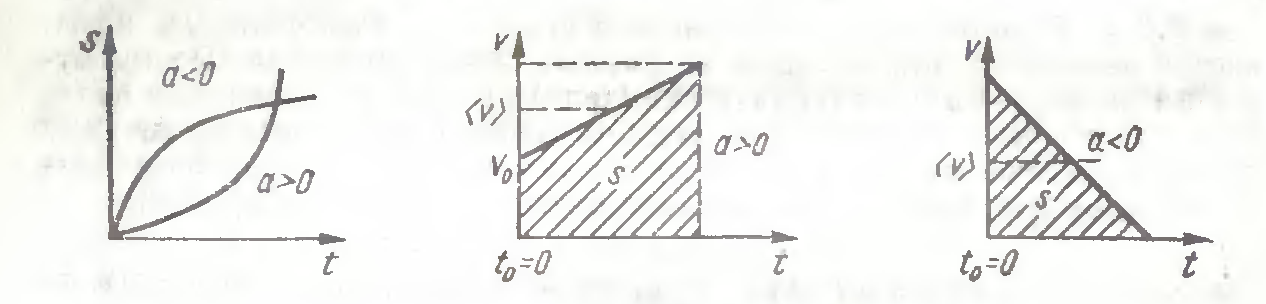
Рисунок 2. Связь между параметрами равноускоренного движения
Учитывая, что равноускоренное движение есть движение поступательное, описывающие его уравнения в векторной и скалярной форме идентичны.
Считая, что t0 = 0, получаем следующие формулы для вычисления пути, пройденного телом при равноускоренном движении за время $t$:
Скорость при равноускоренном движении:
Средняя скорость равноускоренного движения за время t:
Время движения при равноускоренном движении:
Ускорение при равноускоренном движении:
Построить графики зависимости скорости от времени при следующих начальных условиях.
$$I:\ {\upsilon ~}_0=~--2\ {м}/{с},\ \ \ \ a~=\frac{1}{2}~~{м}/{с^2},\ \ \ t=4\ c\ $$ $$ $II:\ {\upsilon }_0~=~3~{м}/{с},\ a~=~--\frac{1}{3}~{м}/{с^2}$, t = 5,5 c $$Показать на этом графике перемещение вычислить его при заданном значении времени $t$
Решение
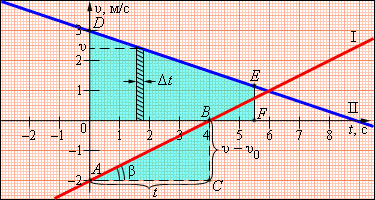
Рисунок 3.
Материальная точка движется по прямой.
Определить мгновенную скорость и среднюю скорость в конце второй секунды от начала движения, и путь, пройденный за это время.
Решение











