
При движении материальной точки изменяются ее координаты. Координаты могут изменяться быстро или медленно. Физическая величина, которая характеризует быстроту изменения координаты, называется скоростью.
Средняя скорость -- это векторная величина, численно равная перемещению в единицу времени, и сонаправленная с вектором перемещения:$\left\langle v\right\rangle =\frac{\triangle r}{\triangle t}$ ; $\left\langle v\right\rangle \uparrow \uparrow \triangle r$
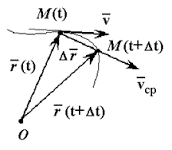
Рисунок 1. Средняя скорость сонаправлена перемещению
Mодуль средней скорости по пути равен: $\left\langle v\right\rangle =\frac{S}{\triangle t}$
Мгновенная скорость дает точную информацию о движении в определенный момент времени. Выражение «скорость тела в данный момент времени» с точки зрения физики не является корректным. Однако понятие мгновенной скорости очень удобно в математических расчетах, и им постоянно пользуются.
Мгновенная скорость (или просто скорость) есть предел, к которому стремится средняя скорость $\left\langle v\right\rangle $ при стремлении промежутка времени $\triangle t$ к нулю:
$v={\mathop{lim}_{\triangle t} \frac{\triangle r}{\triangle t}\ }=\frac{dr}{dt}=\dot{r}$ (1)
Вектор $v$ направлен по касательной к криволинейной траектории, так как бесконечно малое (элементарное) перемещение dr совпадает с бесконечно малым элементом траектории ds.
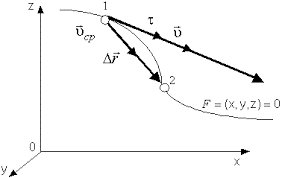
Рисунок 2. Вектор мгновенной скорости $v$
В декартовых координатах уравнение (1) эквивалентно трем уравнениям
$\left\{ \begin{array}{c} v_x=\frac{dx}{dt}=\dot{x} \\ v_y=\frac{dy}{dt}=\dot{y} \\ v_z=\frac{dz}{dt}=\dot{z} \end{array} \right.$ (2)Модуль вектора $v$ в этом случае равен:
$v=\left|v\right|=\sqrt{v^2_x+v^2_y+v^2_z}=\sqrt{x^2+y^2+z^2}$ (3)Переход от декартовых прямоугольных координат к криволинейным осуществляется по правилам дифференцирования сложных функций. Пусть радиус-вектор r есть функция криволинейных координат: $r=r\left(q_1,q_2,q_3\right)\ $. Тогда скорость $v=\frac{dr}{dt}=\sum^3_{i=1}{\frac{\partial r}{\partial q_i}\frac{\partial q_i}{\partial t}}=\sum^3_{i=1}{\frac{\partial r}{\partial q_i}}\dot{q_i}$

Рисунок 3. Перемещение и мгновенная скорость в системах криволинейных координат
В сферических координатах, полагая $q_1=r;\ \ q_2=\varphi ;\ \ q_3=\theta $, получаем представление $v$ в следующий форме:
$v=v_re_r+v_{\varphi }e_{\varphi }+v_{\theta }e_{\theta }$, где $v_r=\dot{r};\ \ v_{\varphi }=r\dot{\varphi }sin\theta ;;\ \ v_{\theta }=r\dot{\theta }\ ;;$ \[\dot{r}=\frac{dr}{dt};;\ \ \dot{\varphi }=\frac{d\varphi }{dt};;\ \ \dot{\theta }=\frac{d\theta }{dt}; v=r\sqrt{1+{\varphi }^2sin^2\theta +{\theta }^2}\]Мгновенная скорость - это значение производной от функции перемещения по времени в заданный момент времени, и связана с элементарным перемещением следующим соотношением: $dr=v\left(t\right)dt$
Закон движения точки по прямой: $x\left(t\right)=0,15t^2-2t+8$. Найти мгновенную скорость точки через 10 секунд после начала движения.
Решение
Мгновенная скорость точки -- это первая производная радиус-вектора по времени. Поэтому для мгновенной скорости можно записать:
\[v\left(t\right)=\dot{x}\left(t\right)=0.3t-2;; v\left(10\right)=0.3\times 10-2=1\ м/с\]Ответ: Через 10 с после начала движения мгновенная скорость точки 1 м/с.
Движение материальной точки задано уравнением~ $x=4t-0,05t^2$. Определить момент времени $t_{ост.}$, в который точка остановится, и среднюю путевую скорость $\left\langle v\right\rangle $.
Решение
Найдем уравнение мгновенной скорости: $v\left(t\right)=\dot{x}\left(t\right)=4-0,1t$
\[4-0,1t=0;;\ \ \ \ \ \ t_{ост.}=40\ c;;\ \ \ v_0=v\left(0\right)=4;;\ \ \ \ \left\langle v\right\rangle =\frac{\triangle v}{\triangle t}=\frac{0-4}{40-0}=0.1\ м/c\ \ \]Ответ: Точка остановится через 40 секунд после начала движения. Средняя скорость её движения 0,1 м/с.











