Если тело бросить под углом к горизонту, то в полете на него действуют сила тяжести и сила сопротивления воздуха. Если силой сопротивления пренебречь, то остается единственная сила -- сила тяжести. Поэтому вследствие 2-го закона Ньютона тело движется с ускорением, равным ускорению свободного падения; проекции ускорения на координатные оси ах = 0, ау = - g.
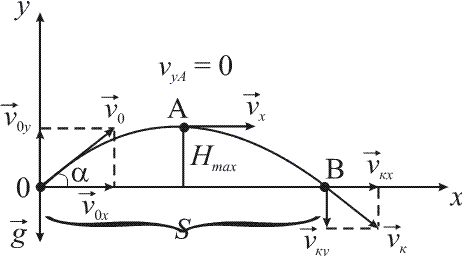
Рисунок 1. Кинематические характеристики тела, брошенного под углом к горизонту
Любое сложное движение материальной точки можно представить как наложение независимых движений вдоль координатных осей, причем в направлении разных осей вид движения может отличаться. В нашем случае движение летящего тела можно представить как наложение двух независимых движений: равномерного движения вдоль горизонтальной оси (оси Х) и равноускоренного движения вдоль вертикальной оси (оси Y) (рис. 1).
Проекции скорости тела, следовательно, изменяются со временем следующим образом:
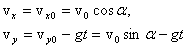
где $v_0$ - начальная скорость, ${\mathbf \alpha }$ - угол бросания.
Координаты тела, следовательно, изменяются так:
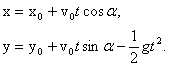
При нашем выборе начала координат начальные координаты (рис. 1) $x_0=y_0=0$. Тогда получим:
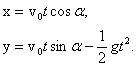 (1)
(1)
Проанализируем формулы (1). Определим время движения брошенного тела. Для этого положим координату y равной нулю, т.к. в момент приземления высота тела равна нулю. Отсюда получаем для времени полета:
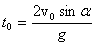 (2)
(2)
Второе значение времени, при котором высота равна нулю, равно нулю, что соответствует моменту бросания, т.е. это значение также имеет физический смысл.
Дальность полета получим из первой формулы (1). Дальность полета - это значение координаты х в конце полета, т.е. в момент времени, равный $t_0$. Подставляя значение (2) в первую формулу (1), получаем:
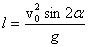 (3)
(3)
Из этой формулы видно, что наибольшая дальность полета достигается при значении угла бросания, равном 45 градусов.
Наибольшую высоту подъема брошенного тела можно получить из второй формулы (1). Для этого нужно подставить в эту формулу значение времени, равное половине времени полета (2), т.к. именно в средней точке траектории высота полета максимальна. Проводя вычисления, получаем
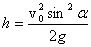 (4)
(4)
Из уравнений (1) можно получить уравнение траектории тела, т.е. уравнение, связывающее координаты х и у тела во время движения. Для этого нужно из первого уравнения (1) выразить время:
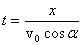
и подставить его во второе уравнение. Тогда получим:
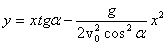
Это уравнение является уравнением траектории движения. Видно, что это уравнение параболы, расположенной ветвями вниз, о чем говорит знак «-» перед квадратичным слагаемым. Следует иметь в виду, что угол бросания $\alpha $ и его функции -- здесь просто константы, т.е. постоянные числа.
Тело брошено со скоростью v0 под углом ${\mathbf \alpha }$ к горизонту. Время полета $t = 2 с$. На какую высоту Hmax поднимется тело?
Решение
Дано:
$$t_В = 2 с$$ $$H_max - ?$$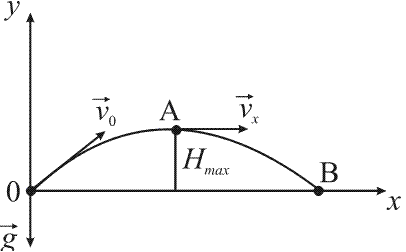
Закон движения тела имеет вид:
$$\left\{ \begin{array}{c} x=v_{0x}t \\ y=v_{0y}t-\frac{gt^2}{2} \end{array} \right.$$Вектор начальной скорости образует с осью ОХ угол ${\mathbf \alpha }$. Следовательно,
С вершины горы бросают под углом = 30${}^\circ$ к горизонту камень с начальной скоростью $v_0 = 6 м/с$. Угол наклонной плоскости = 30${}^\circ$. На каком расстоянии от точки бросания упадет камень?
Решение
Дано:
$$ \alpha =30{}^\circ$$ $$v_0=6\ м/с$$ $$S - ?$$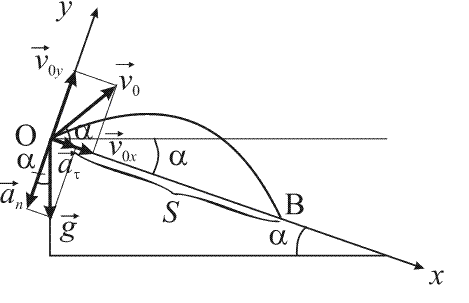
Поместим начало координат в точку бросания, ОХ -- вдоль наклонной плоскости вниз, OY -- перпендикулярно наклонной плоскости вверх. Кинематические характеристики движения:
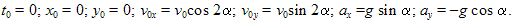
Закон движения:
$$\left\{ \begin{array}{c} x=v_0t{cos 2\alpha +g\frac{t^2}{2}{sin \alpha \ }\ } \\ y=v_0t{sin 2\alpha \ }-\frac{gt^2}{2}{cos \alpha \ } \end{array} \right.$$Подставив полученное значение $t_В$, найдём $S$:











