В соответствии с теорией близкодействия, взаимодействия между заряженными телами, которые удалены друг от друга, осуществляется посредством полей (электромагнитных), создаваемых этими телами в окружающем их пространстве. Если поля создаются неподвижными частицами (телами), то поле является электростатическим. Если поле не изменяется во времени, то его называют стационарным. Электростатическое поле является стационарным. Это поле -- частный случай электромагнитного поля. Силовой характеристикой электрического поля служит вектор напряженности, который можно определить как:
где $\overrightarrow{F}$- сила, действующая со стороны поля на неподвижный заряд q, который называют иногда «пробным». При этом необходимо, чтобы «пробный» заряд был мал, чтобы не искажал поле, напряженность которого с его помощью измеряют. Из уравнения (1) видно, что напряженность совпадает по направлению с силой, с которой поле действует на единичный положительный «пробный заряд».
Напряженность электростатического поля не зависит от времени. Если напряженность во всех точках поля одинакова, то поле называют однородным. В противном случае поле неоднородно.
Силовые линии
Для графического изображения электростатических полей используют понятие силовых линий.
Силовыми линиями или линиями напряженности поля, называются линии, касательные к которым в каждой точке поля совпадают с направлениями векторов напряженности в этих точках.
Силовые линии электростатического поля являются разомкнутыми. Они начинаются на положительных зарядах и заканчиваются на отрицательных. Иногда они могут уходить в бесконечность или приходить из бесконечности. Силовые линии поля не пересекаются.
Вектор напряженности электрического поля подчиняется принципу суперпозиции, а именно:
\[\overrightarrow{E}=\sum\limits^n_{i=1}{{\overrightarrow{E}}_i(2)}.\]Результирующий вектор напряженности поля может быть найден как векторная сумма напряженностей составляющих его «отдельных» полей. Если заряд распределен непрерывно (нет необходимости учитывать дискретность), то суммарная напряженность поля найдется как:
\[\overrightarrow{E}=\int{d\overrightarrow{E}}\ \left(3\right).\]В уравнении (3) интегрирование проводят по области распределения зарядов. Если заряды распределены по линии ($\tau =\frac{dq\ }{dl}$ -линейная плотность распределения заряда), то интегрирование в (3) проводят по линии. Если заряды распределены по поверхности и поверхностная плотность распределения $\sigma=\frac{dq\ }{dS}$, то интегрируют по поверхности. Интегрирование проводят по объему, если имеют дело с объемным распределением заряда: $\rho =\frac{dq\ }{dV}$, где $\rho $ -- объемная плотность распределения заряда.
Напряженность поля
Напряжённость поля в диэлектрике равна векторной сумме напряженностей полей, которые создают свободные заряды ($\overrightarrow{E_0}$) и связанные заряды ($\overrightarrow{E_p}$):
\[\overrightarrow{E}=\overrightarrow{E_0}+\overrightarrow{E_p}\left(4\right).\]Очень часто в примерах мы сталкиваемся с тем, что диэлектрик является изотропным. В таком случае, напряжённость поля может быть записана как:
\[\overrightarrow{E}=\frac{\overrightarrow{E_0}}{\varepsilon }\ \left(5\right),\]где $\varepsilon $- относительная диэлектрическая проницаемость среды в рассматриваемой точке поля. Таким образом, из (5) очевидно, что однородном в изотропном диэлектрике напряженность электрического поля в $\varepsilon $ раз меньше, чем в вакууме.
Напряженность электростатического поля системы точечных зарядов равна:
\[\overrightarrow{E}=\frac{1}{4\pi {\varepsilon }_0}\sum\limits^n_{i=1}{\frac{q_i}{\varepsilon r^3_i}}\overrightarrow{r_i}\ \left(6\right).\]В системе СГС напряженность поля точечного заряда в вакууме равна:
\[\overrightarrow{E}=\frac{q\overrightarrow{r}}{r^3}\left(7\right).\]Задание: Заряд равномерно распределен по четверти окружности радиуса R с линейной плотностью $\tau $. Найти напряженность поля в точке (А), которая была бы центром окружности.
Решение:
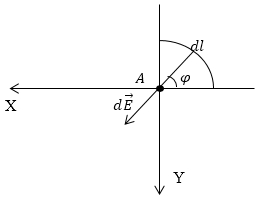
Рис. 1
Выделим на заряженной части окружности элементарный участок ($dl$), который будет создавать элемент поля в точке А, для него запишем выражение для напряженности (будем использовать систему СГС), в таком случае выражение для $d\overrightarrow{E}$ имеет вид:
\[d\overrightarrow{E}=\frac{dq}{R^3}\frac{\overrightarrow{R}}{R}\ \left(1.1\right).\]Проекция вектора $d\overrightarrow{E}$ на ось OX имеет вид:
\[{dE}_x=dEcos\varphi =\frac{dqcos\varphi }{R^2}\left(1.2\right).\]Выразим dq через линейную плотность заряда $\tau $:
\[dq=\tau dl=\tau \cdot 2\pi RdR\ \left(1.3\right).\]Используя (1.3) преобразуем (1.2), получим:
\[{dE}_x=\frac{2\pi R\tau dRcos\varphi }{R^2}=\frac{2\pi \tau dRcos\varphi }{R}=\frac{\tau cos\varphi d\varphi }{R}\ \left(1.4\right),\]где $2\pi dR=d\varphi $.
Найдем полную проекцию $E_x$, интегрированием выражения (1.4) по $d\varphi $, где угол изменяется $0\le \varphi \le 2\pi $.
\[E_x=\int\limits^{2\pi }_0{\frac{\tau cos\varphi d \varphi }{R}}=\frac{\tau }{R}\int\limits^{2 \pi}_0{cos\varphi d \varphi=}\frac{\tau}{R}\left({\left.sin\varphi \right|}^{2\pi }_0\right)=\frac{\tau }{R}\ \left(1.5\right).\]Займемся проекцией вектора напряженности на ос OY, по аналогии без особых пояснений запишем:
\[{dE}_y=dEsin\varphi =\frac{\tau }{R}sin\varphi d \varphi \ \left(1.6\right).\]Интегрируем выражение (1.6), угол изменяется $\frac{\pi }{2}\le \varphi \le 0$, получаем:
\[E_y=\int\limits^0_{\frac{\pi }{2}}{\frac{\tau }{R}sin\varphi d\varphi =\frac{\tau }{R}\int\limits^0_{\frac{\pi }{2}}{sin\varphi d\varphi =-\ \frac{\tau }{R}}\ }{\left.cos\varphi \right|}^0_{\frac{\pi }{2}}=-\ \frac{\tau }{R}\ \left(1.7\right).\]Найдем модуль вектора напряженности в точке А, используя теорему Пифагора:
\[E=\sqrt{{E_x}^2+{E_y}^2}=\sqrt{{\left(\frac{\tau }{R}\right)}^2+{\left(-\frac{\tau }{R}\right)}^2}=\frac{\tau }{R}\sqrt{2}\]Ответ: Напряженность поля в точке (А) равна $E=\frac{\tau }{R}\sqrt{2}.$
Задание: Найдите напряженность электростатического поля равномерно заряженной полусферы, радиус которой равен R. Поверхностная плотность заряда равна $\sigma$.
Решение:
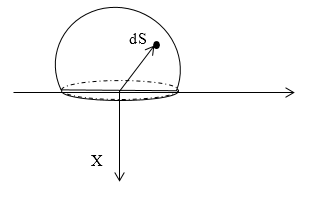
Рис. 2
Выделим на поверхности заряженной сферы элементарный заряд $dq$, который расположен на элементе площади $dS.$ В сферических координатах $dS$ равен:
\[dS=R^2sin\theta d\theta d\varphi \ \left(2.1\right),\]где $0\le \varphi \le 2\pi ,\ 0\le \theta \le \frac{\pi }{2}.$
Запишем выражение для элементарной напряженности поля точечного заряда в системе СИ:
\[d\overrightarrow{E}=\frac{dq}{{4\pi {\varepsilon }_0R}^3}\frac{\overrightarrow{R}}{R}\ \left(2.2\right).\]Проектируем вектор напряженности на ось OX, получим:
\[{dE}_x=\frac{dqcos\theta }{4 \pi \varepsilon_0R^2}\left(2.3\right).\]Элементарный заряд выразим через поверхностную плотность заряда, получим:
\[dq=\sigma dS\ \left(2.4\right).\]Подставляем (2.4) в (2.3), используем (2.1) интегрируем, получаем:
\[E_x=\frac{\sigma R^2}{4\pi {\varepsilon }_0R^2}\int\limits^{2\pi }_0{d\varphi \int\limits^{\frac{\pi }{2}}_0{cos\theta }}sin\theta d\theta =\frac{\sigma}{4\pi {\varepsilon }_0}\left(2\pi \cdot \frac{1}{2}\right)=\frac{\sigma}{4{\varepsilon }_0}.\]Легко получить, что $E_Y=0.$
Следовательно, $E=E_x.$
Ответ: Напряженность поля полусферы заряженной по поверхности в ее центре равна $E=\frac{\sigma}{4{\varepsilon }_0}.$











