
Решение уравнения Пуассона
В достаточно большом количестве случаев наиболее удобным методом поиска напряженности поля является решение дифференциального уравнения для потенциала. Получим его, используя в качестве основы теорему Остроградского - Гаусса в дифференциальной форме:
где $\rho $ -- плотность распределения заряда, ${\varepsilon }_0$ -- электрическая постоянная, $div\overrightarrow{E}=\overrightarrow{\nabla }\overrightarrow{E}=\frac{\partial E_x}{\partial x}+\frac{\partial E_y}{\partial y}+\frac{\partial E_z}{\partial z}$) -- дивергенция вектора напряженности и выражение связывающее напряженность поля и потенциал:
Подставим (2) в (1), получим:
Учитываем, что $divgrad\varphi ={\nabla }^2\varphi =\frac{{\partial }^2\varphi }{\partial x^2}+\frac{{\partial }^2\varphi }{\partial y^2}+\frac{{\partial }^2\varphi }{\partial z^2}$, где $\triangle ={\nabla }^2$- оператор Лапласа, тогда равенство (3) запишем как:
Уравнение (4) называется уравнением Пуассона (для вакуума) в системе СИ. Если заряды отсутствуют, то уравнение (4) преобразуется в уравнение Лапласа:
После того, как найден потенциал из уравнения Пуассона, обычно вычисляется напряженность по формуле (2). Решения уравнения Пуассона должны удовлетворять таким требованиям:
- Потенциал должен быть непрерывной функцией.
- Потенциал должен быть конечной функцией.
- Производные от потенциала как функции по координатам должны быть конечными.
Если заряды сосредоточены в объеме V, то решением уравнения (4) будет выражение для потенциала вида:
Итак, общая задача электростатики сводится к нахождению решения дифференциального уравнения (уравнения Пуассона), которое удовлетворяет выше перечисленным требованиям. Нахождение решения -- задача весьма сложная. Теоретические решения известны для небольшого количества частных случаев. Если удалось подобрать функцию $\varphi $, которая удовлетворяет всем условиям задачи, то она единственная.
Не всегда есть необходимости задавать заряды или потенциалы во всем пространстве. Например, если необходимо найти электрическое поле в полости, которая окружена проводящей оболочкой, то можно найти поле только для тел внутри самой полости.
Каждое решение уравнения Пуассона в ограниченной области однозначно определяется краевыми условиями, которые накладывают на поведение решения. На границе перехода из одной среды в другую выполняются граничные условия:
\[E_{2n}-E_{1n}=4\pi \sigma ,\ или\ \frac{\partial {\varphi }_1}{\partial n}-\frac{\partial {\varphi }_2}{\partial n}=0.\] \[E_{1\tau }=E_{2\tau }.\] \[{\varphi }_1=ц_{2\ }\]где $\sigma $- поверхностная плотность свободных зарядов, n- единичный вектор нормали к границе раздела, проведенный из среды 1 в 2, $\tau -\ $единичный вектор, касательный к границе.
Данные уравнения выражают скачок нормальных составляющих вектора напряженности и непрерывность касательной составляющей вектора напряженностей электрического поля при переходе через любую заряженную поверхность не зависимо от формы этой поверхности и наличия и отсутствия зарядов вне ее.
Уравнение Пуассона в сферических, полярных и цилиндрических координатах
Уравнение Пуассона может быть записано не только в декартовых координатах, но также в сферических и цилиндрических, полярных.
В сферических координатах ($r,\theta ,\vartheta)$ уравнение Пуассона имеет следующий вид:
\[\frac{1}{r^2}\cdot \frac{\partial }{\partial r}\left(r^2\frac{\partial \varphi }{\partial r}\right)+\frac{1}{r^2sin\theta \partial \theta }\left(sin\theta \cdot \frac{\partial \varphi }{\partial \theta }\right)+\frac{{\partial }^2\varphi }{r^2{sin}^2\theta \partial {\varphi }^2}=-\frac{1}{{\varepsilon }_0}\rho \left(7\right).\]В полярных координатах ($r,\theta )$ система координат уравнение имеет вид:
\[\frac{1}{r}\cdot \frac{\partial }{\partial r}\left(r\frac{\partial \varphi }{\partial r}\right)+\frac{{\partial }^2\varphi }{r^2\partial {\theta }^2}=-\frac{1}{{\varepsilon }_0}\rho \left(8\right).\]В цилиндрических координатах ($r,\vartheta,z)$ уравнение имеет вид:
\[\frac{1}{r}\cdot \frac{\partial }{\partial r}\left(r\frac{\partial \varphi }{\partial r}\right)+\frac{{\partial }^2\varphi }{\partial z^2}+\frac{{\partial }^2\varphi }{r^2\partial \vartheta^2}=-\frac{1}{{\varepsilon }_0}\rho \left(9\right).\]Задание: Найдите поле между двумя коаксиальными цилиндрами с радиусами $r_1$ и $r_2$, разность потенциалов между которыми равна $\triangle U={\varphi }_1-{\varphi }_2.$
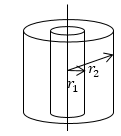
Рис. 1
Решение:
Запишем уравнение Лапласа в цилиндрических координатах с учетом аксиальной симметрии:
$\frac{1}{r}\cdot \frac{\partial }{\partial r}\left(r\frac{\partial \varphi }{\partial r}\right)=0$(1.1)
Оно имеет решение $\varphi =-Aln(r)$+B. Выберем нулевой потенциал на наружном цилиндре, найдем, получим:
$\varphi \left(r_2\right)=0=-Alnr_2+B,$ следовательно
\[B=Alnr_2.\ \] $\varphi \left(r_1\right)=\triangle U=-Alnr_1+B$, получим: \[A=\frac{\triangle U}{{ln \left(\frac{r_2}{r_1}\right)\ }}.\]В результате имеем: $\varphi (r)=-\frac{\triangle U}{{ln \left(\frac{r_2}{r_1}\right)\ }}ln\left(r\right)+\frac{\triangle U}{{ln \left(\frac{r_2}{r_1}\right)\ }}lnr_2$
Ответ: Поле между двумя коаксиальными цилиндрами задается функцией $\varphi (r)=-\frac{\triangle U}{{ln \left(\frac{r_2}{r_1}\right)\ }}ln\left(r\right)+\frac{\triangle U}{{ln \left(\frac{r_2}{r_1}\right)\ }}lnr_2$
Задание: Найти, используя уравнение Пуассона потенциал поля, которое создает бесконечно длинный круглый цилиндр радиуса R с объемной плотностью заряда $\rho $.
Решение:
Ось Z направим по оси цилиндра. Так как цилиндрическое распределение заряда аксиально симметрично, то потенциал обладает той же симметрией, то есть он является функцией $\varphi \left(r\right),\ $где r -- расстояние от оси цилиндра. Поэтому используем цилиндрическую систему координат. Запишем уравнение Пуассона в ней с учетом симметрии:
\[\frac{1}{r} \cdot \frac{\partial}{\partial r} \left(r\frac{\partial {\varphi }_1}{\partial r}\right)=- \frac{1}{ \varepsilon_0} \rho \ \left(0 Общие решения уравнений (2.1) (2.2) имеют вид: \[{\varphi }_1=-\frac{1}{4}\frac{\rho }{{\varepsilon }_0}r^2+C_1lnr+{C'}_1\left(2.3\right),\] \[{\varphi }_2=C_2lnr+{C'}_2\left(2.4\right),\]где $C_1$,$\ {C'}_1,C_2$,$\ {C'}_2$ -- постоянные интегрирования. Так как потенциал во всех точках должен быть конечным, а ${\mathop{lim}_{r\to 0} lnr\ }=\infty $, следовательно, $C_1=0.$ Пронормируем потенциал условием:${\varphi }_1\left(0\right)=0$, тогда: ${C'}_1=0.$
Так как поверхностных зарядов нет, то напряженность электрического поля на поверхности шара непрерывна, то есть непрерывна производная от потенциала при r=R. И непрерывен сам потенциал. Эти условия дают два алгебраических уравнения для того, чтобы найти постоянные $C_2$,$\ {C'}_2:$
\[C_2lnR+{C'}_2=-\frac{1}{4}\frac{\rho }{{\varepsilon }_0}R^2(2.5)\] \[\frac{C_2}{R}=-\frac{1}{2}\frac{\rho }{{\varepsilon }_0}R\left(2.6\right).\]Следовательно, получаем выражения для потенциалов:
\[{\varphi }_1\left(r\right)=-\frac{1}{4}\frac{\rho }{{\varepsilon }_0} r ^ 2 \left(0 Ответ: Потенциал поля равен: $$ \varphi_1 \left(r \right)=-\frac{1}{4}\frac{\rho }{\varepsilon_0} r^2 \left (0










