Что такое сегнетоэлектрики
Сегнетоэлектрики это диэлектрики, которые обладают рядом специфических свойств, которые реализуются благодаря тому, что обладают доменной структурой и в некоторой области температур могут спонтанно поляризоваться, причем направление этой поляризации можно изменить с помощью электрического поля.
В некоторых твердых и жидких веществах при определенных внешних воздействиях происходят фазовые превращения без изменения их агрегатных состояний. Например, сегнетоэлектрик может превращаться в параэлектрик.
Что такое точка Кюри
Если повышать температуру сегнетоэлектрика до некоторой температуры ($T_k$), которая своя для каждого вещества, то сегнетоэлектрические свойства диэлектрика исчезают, и он становится обычным диэлектриком. Такая точка фазового перехода из состояния сегнетоэлектрика в состояние полярного диэлектрика называется точкой Кюри, а соответствующая температура ($T_k$) - температурой Кюри. Существуют сегнетоэлектрики, у которых две точки Кюри, верхняя и нижняя. Такие вещества сохраняют свои сегнетоэлектрические свойства в интервале температур, которые заданы верхней и нижней границами. Таких сегнетоэлектриков сравнительно не много. У большинства сегнетоэлектриков только верхняя точка Кюри.
График зависимости спонтанной поляризации сегнетоэлектрика ($P_S$) от температуры вблизи точки Кюри приведен на рис.1.
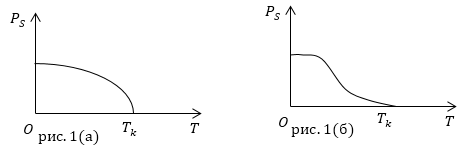
В окрестности фазового превращения (в точке Кюри) структура вещества сегнетоэлектрика оказывается податлива к внешним воздействиям. Даже небольшие изменения напряженности поля вблизи фазового перехода вызывают существенные изменения электрических свойств диэлектрика.
Вблизи точки Кюри у сегнетоэлектриков, находящихся в полярной фазе, значения диэлектрической проницаемости достигают очень больших значений, (вплоть до ${10}^4-\ {10}^5)$. Например, у титаната бария $(BaTiO_3)$ точка Кюри лежит около температуры $120^oC$, а диэлектрическая проницаемость достигает в максимуме $6000-7000$. Надо отметить, что существуют сегнетоэлектрики и с не очень большой диэлектрической проницаемостью, например, некоторые водорастворимые сегнетоэлектрики имеют проницаемость $\varepsilon =5-6$.
Причем максимум диэлектрической проницаемости достигается в точке Кюри (рис.2).
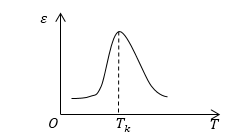
Рис. 2
Закон изменения диэлектрической восприимчивости
Закон изменения диэлектрической восприимчивости в неполярной фазе сегнетоэлектрика около точки Кюри можно записать как:
где $A$ -- постоянная. $T_0$ -- температура Кюри -- Вейсса, близкая к температуре точки Кюри ($T_k$). Очень часто в формуле (1) вместо $T_0$ используют $T_k$. В том случае, если у сегнетоэлектрика есть две точки Кюри, то вблизи второй точки закон Кюри-Вейсса запишется как:
\[\varkappa =\frac{A'}{{T'}_0-T}\left(2\right).\]В случае неизотропных диэлектриков скалярная величина $\varkappa $ в формулах (1) и (2) должна быть заменена на тензор ${\varkappa }_{ij}.$ Температурная зависимость при этом не изменится.
На практике для сегнетоэлектриков закон Кюри-Вейсса можно записать для нахождения диэлектрической проницаемости в виде:
\[\varepsilon =\frac{С}{T-T_k}\left(3\right),\]где $С=\frac{1}{\alpha T_k}$ -- постоянная Кюри-Вейсса, $T_k$ -- температура Кюри, при которой происходит фазовый переход, а $\alpha $ изменяет знак. Если $С\sim {10}^3$, то фазовый переход происходит с упорядочением некоторых структурных элементов, ионов, протонов или групп атомов. Такой переход иногда называют: порядок -- беспорядок. Если $С\sim {10}^5$, то переход типа смещения относительно положения равновесия. Постоянную Кюри -- Вейсса часто определяют из графика зависимости $\frac{1}{\varepsilon }=\frac{1}{\varepsilon }\left(T\right).$
Надо сказать, что разные сегнетоэлектрики могут обладать фазовыми переходами, как первого, так и второго рода. К сегнетоэлектрикам с фазовым переходом первого рода (рис. 1(а)) относят такие, которые испытывают скачки поляризации при постоянных температуре и давлении:
\[P_i=-{\left(\frac{\partial Ф}{\partial E_i}\right)}_{T,p}\left(4\right),\]где $Ф$ -- термодинамический потенциал, равный:
\[Ф=U-TS+pV-PE\ \left(5\right).\]К сегнетоэлектрикам с фазовым переходом второго рода (рис.2(а)) относят диэлектрики, у которых скачком изменяется диэлектрическая восприимчивость (?) при постоянных давлении и температуре:
\[\varkappa =-{\left(\frac{{\partial }^2Ф}{\partial {E_i}^2}\right)}_{p,T}\left(6\right).\]Наличие точки Кюри является характерным свойством всех сегнетоэлектриков.
Задание: Для гидрофосфата калия ($KH_2PO_4$) который является сегнетоэлектриком, поляризация в котором обусловлена смещением ионов водорода при температурах неблизких к точке Кюри, опыт дает:
\[\varepsilon =4,5+\frac{3100}{T-121}(1.1).\]Определите, значения каких величин, представлены в выражении (1.1)? Найдите коэффициент внутреннего поля $\beta ,$ используя формулу (1.2):
\[\beta =\frac{4\pi T_k}{C-T_k\left({\varepsilon }_0-1\right)}\left(1.2\right).\]Решение:
За основу решения задачи примем формулу, которая определяет связь диэлектрической проницаемости сегнетоэлектрика с температурой:
\[\varepsilon ={\varepsilon }_0+\frac{С}{T-T_k}\left(1.3\right).\]Тогда, сравнивая выражения (1.3) и (1.1) получаем:
\[{\varepsilon }_0=4,5;\ С=3100;\ T_k=121К.\]В таком случае коэффициент $\beta $ легко вычислить, используя (1.2). Получим:
\[\beta =\frac{4\cdot 3,14\cdot 121}{3100-121\left(4,5-1\right)}=0,567\]Ответ: $\beta =0,567$.
Задание: Даны два графика зависимости $\varepsilon $(T) и $\frac{1}{\varepsilon }\left(T \right)$ рис.3 (а,б). Определите, к какой фазе сегнетоэлектрика относятся части графиков I и II.
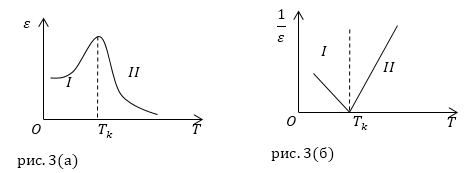
Рис. 3
Решение:
Рассмотрим график рис. 3(а). Отрезок кривой, обозначенный цифрой I, соответствует сегнетоэлектрической фазе диэлектрика, в точке Кюри ( $T_k$) поляризация достигает максимума, отрезок с цифрой II соответствует пароэлектрической фазе диэлектрика. Диэлектрическая проницаемость резко падает, с ростом температуры разрушается доменная структура вещества.
Рассмотрим график рис. 3(б). В соответствии с законом Кюри-Вейсса:
\[\varepsilon =\frac{С}{T-T_k}\left(2.1\right),\]следовательно:
\[\frac{1}{\varepsilon }=\frac{T-T_k}{С}\left(2.2\right).\]Отрезок I, относится к фазе -- сегнетоэлектрик. Величина, обратная к диэлектрической проницаемости, линейно уменьшается с ростом температуры, вплоть до $T>T_k$, при $T=T_k$ $\frac{1}{\varepsilon }=0$. Далее отрезок II - параэлектрик при температуре выше, чем точка Кюри.












