Величина и дипольный момент объема
В том случае, если диэлектрик не поляризован, то объемная и поверхностная плотности связанных зарядов равны нулю. В результате процесса поляризации поверхностная плотность всегда отлична от нуля, а объемная лишь иногда. Между поляризованностью (вектором поляризации $\overrightarrow{P}$) и поверхностной плотностью связанных зарядов ($\sigma $) существует несложная связь. Для того, чтобы ее найти, рассмотрим плоскопараллельную пластину из однородного диэлектрика, которая находится в электростатическом поле (рис.1). Выделим в этой пластине элемент объема в виде тонкого цилиндра. Его ось будет параллельна вектору напряженности поля. Основания цилиндра имеют площадь $\triangle S$, они совпадают с поверхностями цилиндра.
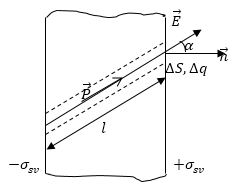
Рис. 1
Величина выделенного объема равна:
где $l$ -- высота цилиндра, $\alpha $ -- угол между направлением вектора напряженности и вектором внешней нормали к поверхности с положительным зарядом. Дипольный момент выделенного объема равен:
Рассматриваемый объем эквивалентен диполю, заряды которого равны $q=\pm {\sigma }_{sv}\triangle S$ и плечо равно l. Электрический момент этого диполя равен $p_e={\sigma }_{sv}\triangle Sl$. $P=p_e$, значит:
Из формулы (3) мы видим искомое выражение, которое связывает поверхностную плотность связанных зарядов и модуль вектора поляризации:
где $P_{n\ }$ - проекция вектора поляризации на внешнюю нормаль к соответствующей поверхности. В нашем случае (рис.1) $P_{n\ }>0$ для правой поверхности, где ${\sigma }_{sv}>0$, для левой: $P_{n\ }
Поверхностная плотность связанных зарядов
Формула (4) справедлива в самом общем случае, когда неоднородный диэлектрик любой формы находится в неоднородном электрическом поле. Под $P_{n\ }$ в таком случае понимают нормальную составляющую вектора, который берется близко к элементу поверхности, для которого определяют поверхностную плотность связанных зарядов.
Итак, поверхностная плотность связанных зарядов на границе раздела двух диэлектриков равна:
\[{\sigma }_{sv}=P_{1n\ }-P_{2n}=-\overrightarrow{n_{12}}\left(\overrightarrow{P_2}-\overrightarrow{P_1}\right)\left(5\right),\]где $\overrightarrow{n_{12}}$ -- единичный вектор нормали, который направлен из первого диэлектрика во второй.
Плотность объемных связанных зарядов так же связана с вектором поляризации, а именно:
\[{\rho }_{sv}=-div\overrightarrow{P}\left(6\right).\]Формула (6) имеет следующий смысл: Точки с положительной дивергенцией вектора поляризации служат источниками поля вектора $\overrightarrow{P}$, из таких точек линии поля расходятся. Точки с отрицательной дивергенцией $\overrightarrow{P}$ служат стоками поля вектора поляризации, к этим точкам линии сходятся. Это означает, что при поляризации диэлектрика связанные заряды, которые имею знак плюс, смещаются в направлении вектора $\overrightarrow{P}$, вернее, в направлении линий его поля. Отрицательные заряды смещаются в противоположном направлении. Как следствие, в местах положительной дивергенции вектора поляризации имеется избыток отрицательных связанных зарядов, а в местах с отрицательной дивергенцией $\overrightarrow{P}$ -- избыток положительных зарядов.
Задание: Пластины плоского конденсатора заряжены с поверхностной плотностью заряда ?. Между пластинами конденсатора находятся две диэлектрические пластины, проницаемость которых равна ${\varepsilon }_1$ и ${\varepsilon }_2$. Они плотно прилегают друг к другу. Определить плотности связанных зарядов пластин из диэлектрика на границе их раздела ($\sigma '$).
Решение:
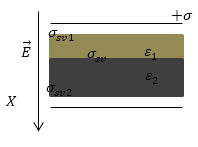
Рис. 2
Основой для решения задачи служит уравнение -- граничное условие для перехода вектора поляризации через границу двух диэлектриков:
\[{\sigma }_{sv}=P_{1n\ }-P_{2n}\left(1.1\right).\]Напряженности поля равны, вне диэлектрика:
\[E_{vak}=\frac{\sigma }{{\varepsilon }_0}\left(1.2\right),\]внутри первого диэлектрика:
\[E_1=\frac{\sigma }{{\varepsilon }_1{\varepsilon }_0}\left(1.3\right),\]внутри второго диэлектрика:
\[E_2=\frac{\sigma }{{\varepsilon }_2{\varepsilon }_0}\left(1.4\right).\]Зная, что вектор поляризации в случае изотропного диэлектрика связан с напряженностью соотношением:
\[P={\varepsilon }_0\varkappa E\ \left(1.5\right).\]Используя (1.3), (1.4) и (1.5) запишем:
\[P_1=\frac{{\varkappa }_1\sigma }{{\varepsilon }_1}\left(1.6\right),\] \[P_2=\frac{{\varkappa }_2\sigma }{{\varepsilon }_2}\left(1.7\right).\]Найдем поверхностные плотности связанных зарядов для первого диалектика (верхняя) свободная поверхность:
\[{\sigma }_{sv1}=-P_1=-\sigma \left(1-\frac{1}{{\varepsilon }_1}\right)\left(1.8\right).\]для второго диалектика (нижняя) свободная поверхность:
\[{\sigma }_{sv2}=P_2=-\sigma \left(1-\frac{1}{{\varepsilon }_2}\right)\left(1.9\right).\]На границе раздела двух диэлектриков получим, что поверхностная плотность зарядов равна:
\[{\sigma }_{sv}=-у_{sv1}-у_{sv2}=\frac{\varepsilon_1-\varepsilon_2}{\varepsilon_1 \varepsilon_2}\sigma \left(1.10\right).\]Ответ: ${\sigma }_{sv}=\frac{\varepsilon_1-\varepsilon_2}{\varepsilon_1 \varepsilon_2}у.$
Задание: Бесконечная пластина из однородного, изотропного диэлектрика с диэлектрической проницаемостью$\ \varepsilon $ заряжена равномерно сторонними зарядами, объемная плотность распределения этого заряда равна $\rho $. Толщина пластины 2а. Найдите объемную плотность связанных зарядов. Диэлектрическая проницаемость вещества вне пластины равна единице.
Решение:
Для бесконечной пластины диэлектрика напряженность поля зависит от одной координаты. Допустим, что ось X направлена перпендикулярно к плоскости пластины и ее начало совпадает с центром слоя диэлектрика. Напряженность бесконечной пластины легко находится из теоремы Остроградского - Гаусса и она равна:
\[\left\{ \begin{array}{c} E=\frac{\rho x}{{\varepsilon \varepsilon }_0},|x| a \end {array} \right.\left(2.1\right),\]где $\sigma$=$\rho \cdot a$ -- поверхностная плотность заряда
Используя уравнение:
\[P={\varepsilon }_0\varkappa E\ \left(2.2\right).\]Найдем модуль вектора поляризации:
\[\left\{ \begin{array}{c} P=\frac{\rho \varkappa x}{\varepsilon},|x| a \end{array} \right.\left(2.3\right),\]Объемная плотность связанных зарядов равна:
\[{\rho }_{sv}=-div\overrightarrow{P}\left(2.4\right).\]Для нашего случая (2.4) преобразуется в:
\[{\rho }_{sv}=-\frac{dP}{dx}=-\frac{\rho \varkappa}{\varepsilon },\]где $\varepsilon =1+\varkappa ,\ \to \varkappa =\varepsilon -1$.
Ответ: ${\rho }_{sv}=-\frac{с(\varepsilon -1)}{\varepsilon}.$











