Электростатическая индукция
Когда мы вносим проводник в электрическое поле, происходит разделение положительных зарядов (ядер) и отрицательных (электронов). Такое явление носит название электростатической индукции. Заряды, которые появляются в результате, называют индуцированными. Индуцированные заряды создают дополнительное электрическое поле.
Поле индуцированных зарядов направлено в сторону противоположную направлению внешнего поля. Поэтому заряды, которые накапливаются на концах проводника, ослабляют внешнее поле. Перераспределение зарядов идет, пока не выполнены условия равновесия зарядов для проводников.
Для того чтобы заряд на проводнике находился в состоянии равновесия необходимо, чтобы:
- Напряженность поля везде внутри проводника была равна нулю, то есть: \[\overrightarrow{E}=0\ \left(1\right).\]
- Вектор $\overrightarrow{E}$ поля на поверхности проводника должен быть направлен перпендикулярно поверхности проводника в каждой точке поля. То есть, если заряд находится в равновесии, поверхность проводника будет эквипотенциальной.
Что означает, что потенциал поля внутри проводника не изменяется. Объем проводника является эквипотенциальным.
Допустим, что мы зарядили проводник до некоторого заряда q. Он распределится так, чтобы заряд находился в равновесии (то есть будут выполняться вышеприведенные условия). Выделим замкнутую поверхность в пределах указанного тела. Так как поле внутри проводника нет, то поток вектора напряженности через избранную поверхность будет равен нулю. Согласно теореме Гаусса -- Остроградского зарядов внутри поверхности нет, их сумма равна нулю. Так ка поверхность мы выбирали произвольно, то при равновесии внутри проводника нигде не может быть зарядов. Заряды распределятся по поверхности с некоторой плотностью распределения $\sigma$. Так как внутри проводника некомпенсированных зарядов нет, то если мы удалим вещество из объема внутри проводника, то это ни как не отразится на равновесии зарядов. На поверхности полости в состоянии равновесия избыточные заряды находиться не могут.
Истечение заряда с острия
Если расстояние от проводника много больше, чем его геометрические размеры, то рисунок линий поля похож на поле точечного заряда. Эквипотенциальные поверхности имеют форму сферы (как у точечного заряда). При приближении к проводнику эквипотенциальные поверхности становятся все более похожи на поверхность проводника, которая, как уже говорилось, является эквипотенциальной. Вблизи выступов эквипотенциальные поверхности расположены гуще, напряженность поля больше. Следовательно, плотность заряда на выступах особенно большая. Так, напряженность поля на острие может быть настолько велика, что может возникать ионизация молекул газа, который окружает проводник.
Ионы газа противоположного знака заряда (относительно заряда проводника) притягиваются к проводнику, нейтрализуют его заряд. Ионы того же знака отталкиваются от проводника, «тянут» за собой нейтральные молекулы газа. Такое явление называют электрическим ветром.
Заряд проводника уменьшается в результате процесса нейтрализации, он как бы стекает с острия. Такое явление называют истечением заряда с острия.
Электрическое смещение поля в однородном изотропном диэлектрике около заряженного проводника равно:
\[D=\sigma \left(2\right),\]где $\sigma$ -- поверхностная плотность распределения зарядов, которая зависит от кривизны поверхности.
А напряженность поля при этом равна:
\[E=\frac{\sigma}{\varepsilon {\varepsilon }_0}\ \left(3\right),\]где ${\varepsilon }_0$ -- электрическая постоянная, $\varepsilon $ -- диэлектрическая проницаемость среды.
На элемент поверхности проводника площади $dS$ действует сила $dF$, которую можно вычислить по формуле:
\[dF=\frac{\sigma^2dS\ }{\varepsilon {\varepsilon }_0}=\frac{\varepsilon {\varepsilon }_0E^2dS}{2}\ \left(4\right),\]где $\overrightarrow{E}\ $напряженность поля в диэлектрике, в точке, где находится проводник. Причем $\overrightarrow{dF}$ направлена в сторону внешней нормали к поверхности проводника.
Задание: Опишите, то происходит с линиями поля, если внести проводник, не обладающий зарядом в электростатическое поле.
Решение:
Если мы вносим нейтральный проводник в электрическое поле, происходит разделение положительных и отрицательных зарядов, то есть на нем образуются индуцированные заряды. Перераспределение зарядов происходит до момента выполнения условий о равенстве нулю напряженности внутри проводника, и перпендикулярности вектора напряженности поля, поверхности проводника. Так, нейтральный проводник как бы разрывает часть линий напряженности поля, он заканчиваются на отрицательных индуцированных зарядах, которые возникли на поверхности проводника и снова начинаются на положительных. Индуцированные заряды распределяются по поверхности проводника (рис.1). Если внутри проводника имеется полость, то в равновесии поле внутри нее равно нулю.
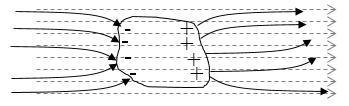
Рис. 1
Задание: Положительный точечный заряд создает электростатическое поле. В это поле внесли шар, который является проводником. Какими будут эквипотенциальные поверхности и силовые линии результирующего поля?
Решение:
Когда в поле вносим незаряженный проводящий шар, то на нем индуцируются заряды, которые распределяются по поверхности шара так, чтобы поле внутри шара было равно нулю, а линии напряженность были перпендикулярны к любой точке шара. Изображение распределения индуцированных зарядов дано на рис.2.
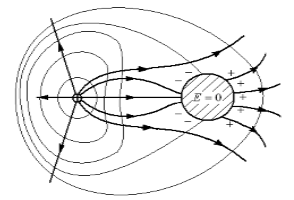
Рис. 2
Силовые линии поля при удалении от заданной системы приближаются по виду к радиальным. Эквипотенциальные поверхности результирующего поля становятся сферами.
Задание: Получите формулу напряжённости поля в вакууме около поверхности заряженного проводника, если положительный заряд распределен по поверхности проводника с поверхностной плотностью $\sigma$.
Решение:
Для выполнения задания используем теорему Остроградского -- Гаусса. Выделим небольшую цилиндрическую поверхность на поверхности проводника так, чтобы ось цилиндра была перпендикулярна поверхности (рис. 3).
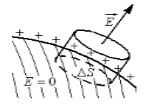
Рис. 3
Линии напряженности поля перпендикулярны поверхности проводника и параллельны оси цилиндра. Поток вектора напряженности через площадку $\triangle S$ (внешнее основание цилиндра) по теореме Остроградского -- Гаусса равен:
\[E\triangle S=\frac{q}{{\varepsilon }_0}\ \left(3.1\right),\]где заряд находящийся внутри выделенной поверхности равен:
\[q=\sigma \cdot \triangle S\ \left(3.2\right),\]Подставляем (3.2) в уравнение (3.1), выражаем напряженность поля, получаем:
\[E\triangle S=\frac{\sigma \cdot \triangle S}{{\varepsilon }_0}\to E=\frac{\sigma}{{\varepsilon }_0}\ .\]Ответ: $E=\frac{\sigma}{{\varepsilon }_0}.$ Причем, если заряд положительный ($\sigma>0$), то вектор напряженности направлен от поверхности, если $\sigma












