Теорема Остроградского - Гаусса
Одним из фундаментальных уравнений электростатики является теорема Остроградского - Гаусса:
«Поток вектора электрического смещения ($Ф_D$) (электрической индукции) через замкнутую поверхность равен сумме свободных зарядов ($q_i$), которые находятся внутри этой поверхности)».
Математическая форма записи интегральной форме этой теоремы для электрического поля в диэлектрике выглядит следующим образом (система СИ):
\[Ф_D=\oint\limits_S{D_ndS}=\sum{q_i=}Q\ \left(1\right),\]где $D_n$ -- нормальная составляющая вектора электрического смещения, $dS$ -- элемент поверхности, через которую ищется поток вектора $\overrightarrow{D}$.
В дифференциальном виде эта же теорема выглядит следующим образом:
\[div\overrightarrow{D}=\rho \ \left(2\right),\]где $\rho $ -- объемная плотность свободных зарядов. Выражения (1) и (2) справедливы не только в электростатике, они выполняются и для переменных полей. Уравнения (1) и (2) являются составной частью системы фундаментальных уравнений Максвелла для электродинамики.
В вакууме поле можно охарактеризовать одним вектором напряженности уравнения (1) или (2) записываются для него и их достаточно. В таком случае, если к ним добавляется теорема о циркуляции вектора напряженности:
\[\oint\limits_L{\overrightarrow{E}d\overrightarrow{s}=0\ \left(3\right),}\]где $\overrightarrow{E}$ -- вектор напряженности электрического поля, $d\overrightarrow{s}$ -- элемент перемещения вдоль контура L. Интеграл в левой части уравнения (3) есть циркуляция вектора напряженности по контуру L. Характерным свойством электростатического поля является то, что циркуляция его вектора напряжённости по любому замкнутому контуру равна нулю.
В вакууме уравнения (1 или 2) и (3) образуют полную систему уравнений электростатики. В веществе этих уравнений не достаточно, так как необходимо описать поведение самой среды в электрическом поле. Следовательно, к выше названным уравнениям электростатики добавляют еще одно векторное уравнение, которое называют материальным уравнением. Оно связывает вектор напряженности поля ($\overrightarrow{E}$) и вектор электрического смещения ($\overrightarrow{D}$) или вектор напряженности поля и вектор поляризации ($\overrightarrow{P}$).
В основном, способ получения такого уравнения содержится уже в определении $\overrightarrow{P}$. Так как если нам известна атомная структура вещества, то можно рассчитать, как смещаются электроны и атомные ядра под воздействием электрического поля. Значит, можно вычислить вектор поляризации и таким образом получить нужное нам уравнение. Однако если идти данным путем, то в зависимости от конкретных условий могут получаться весьма разные соотношения, что неудобно.
Опыты показали, что для большого класса диэлектриков и широкого круга явлений связь между векторами поляризации ($\overrightarrow{P}$) и напряженности ($\overrightarrow{E}$) линейна и однородна, то есть:
\[\overrightarrow{P}=\varkappa {\varepsilon }_0\overrightarrow{E}\ \left(4\right),\]где $\varkappa $ -- диэлектрическая восприимчивость (безразмерная величина), уравнение записано в системе СИ. Такая связь между векторами $\overrightarrow{P}$ и $\overrightarrow{E}$ объясняется тем, что напряженности макроскопических полей невелики в сравнении с напряженностями внутри молекул и атомов. Уравнение выполняется, если диэлектрик изотропен. В таком случае векторы напряженности и поляризуемости коллинеарные. Коэффициент $\varkappa \ $зависит от плотности диэлектрика и температуры.
В анизотропных диэлектриках направление вектора напряженности и вектора поляризации не совпадают. И их связь устанавливается в виде:
\[P_i={\varepsilon }_0\sum\limits_j{{\varkappa }_{ij}E_j\left(5\right),}\]где индексы i,j -- нумеруют компоненты по осям декартовой системы координат ($i=x,\ y,z;j=x,\ y,z$), ${\varkappa }_{ij}$ -- тензор диэлектрической восприимчивости.
По определению, вектор $\overrightarrow{D}\$ равен:
\[\overrightarrow{D}={\varepsilon }_0\overrightarrow{E}+\overrightarrow{P}\left(6\right).\]Следовательно, для изотропного диэлектрика используем (4), запишем:
\[\overrightarrow{D}={\varepsilon }_0\overrightarrow{E}+\varkappa {\varepsilon }_0\overrightarrow{E}=\left(1+\varkappa \right){\varepsilon }_0\overrightarrow{E}=\varepsilon {\varepsilon }_0\overrightarrow{E}\left(7\right),\]где $\varepsilon $ -- диэлектрическая проницаемость среды.
Материальные уравнения для векторов электрического поля
Итак, уравнения:
\[\overrightarrow{D}=\varepsilon {\varepsilon }_0\overrightarrow{E},\] \[\overrightarrow{P}=\varkappa {\varepsilon }_0\overrightarrow{E}\ \left(8\right).\]называют материальными уравнениями для векторов электрического поля.
Эти соотношения, несмотря на их значимость, являются приближенными и не относятся к фундаментальным, так как область применения их ограничена. Существуют вещества, к которым уравнения (8) не применимы. Например, ионные кристаллы могут быть поляризованы в отсутствии внешнего поля. Поведение же, например, электретов (веществ, которые длительное время сохраняют состояние поляризации в отсутствии электрического поля) можно охарактеризовать вектором поляризации, который с вектором напряженности связан уравнением:
\[\overrightarrow{P}=\overrightarrow{P_0}+\varkappa \overrightarrow{E}\left(9\right),\]где $\overrightarrow{P_0}$ и $\varkappa $ не зависят от напряженности поля.
Задание: Бесконечная пластина из однородного, изотропного диэлектрика с диэлектрической проницаемостью$\ \varepsilon $ заряжена равномерно сторонними зарядами, объемная плотность распределения этого заряда равна $\rho $. Толщина пластины 2а. Найдите поляризованность диэлектрика как функцию х (рис.1). Вне пластины диэлектрическую проницаемость среды считать равной единице.
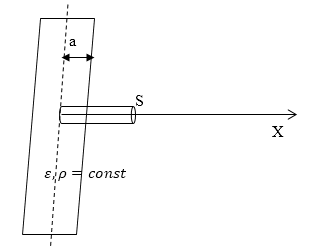
Рис. 1
Решение:
Для бесконечной пластины диэлектрика напряженность поля зависит от одной координаты (в нашем случае - x). Допустим, что ось X направлена перпендикулярно к плоскости пластины и ее начало совпадает с центром слоя диэлектрика. Напряженность бесконечной пластины легко находится из теоремы Остроградского -- Гаусса. Выберем в качестве поверхности, поток через которую будем искать прямой цилиндр, ось которого параллельна оси X (рис.1)площадь основания равна $S$. В таком случае поток вектора напряженности для точек внутри пластины ($\ при\ |x| \[Ф_E=E\cdot S=\frac{q}{\varepsilon {\varepsilon }_0}=\frac{\rho Sx}{\varepsilon {\varepsilon }_0}\ \left(1.1\right),\]
где x -- высота цилиндра для внутренности пластины она изменяется от $-a напряженность поля равна:
Мы получили:
\[ \left\{ \begin{array}{c} E=\frac{\rho x}{\varepsilon \varepsilon_0}, |x| a \end{array} \right.\left(1.4\right) \]Силовые линии, создаваемые полем пластины, направлены вдоль оси X.
Зная, что диэлектрик изотропный, используем связь напряженности и вектора поляризации, учитываем, что вне плоскости связанных зарядов нет:
\[\overrightarrow{P}=\varkappa {\varepsilon }_0\overrightarrow{E}\ \left(1.5\right).\]Найдем модуль вектора поляризации:
\[\left\{ \begin{array}{c} P=\frac{\rho \varkappa x}{\varepsilon }=(1-\frac{1}{\varepsilon })\rho x, |x| a \end{array} \right.\left(1.6\right),\ \]где $\varepsilon =1+\varkappa ,\ \to \varkappa =\varepsilon -1$. По направлению вектор поляризации будет совпадать с вектором напряженности.
Ответ: $\left\{ \begin{array}{c} P=\left(1-\frac{1}{\varepsilon }\right)\rho x, |x| a. \end{array} \right.$
Задание: На рис. 2 изображена картина линий вектора $\overrightarrow{D}\ $при переходе их одного диэлектрика (${\varepsilon }_1$) в другой $({\varepsilon }_2)$. Какая из диэлектрических проницаемостей среды больше?
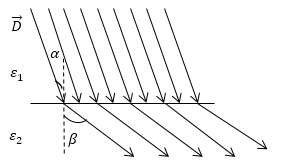
Рис. 2
Решение:
Рассмотрим, как ведут себя силовые линии при прохождении через границу раздела двух диэлектриков. В том случае, если на границе нет свободных зарядов, то должны выполняться граничные условия:
Для тангенциальной составляющей напряженности поля:
\[E_{\tau 1}=E_{\tau 2}\left(2.1\right).\]и нормальной составляющей:
\[{{\varepsilon }_1E}_{n1}={\varepsilon }_2E_{n2}\left(2.2\right).\]Если использовать функции углов, которые показаны на рис. 1, то получим:
\[E_1sin\alpha =E_2sin\beta \ \left(2.3\right).\] \[{{\varepsilon }_1E}_1cos\alpha ={\varepsilon }_2E_2cos\beta \left(2.4\right).\]Зная связь между напряженностью и вектором смещения для изотропного диэлектрика:
\[\overrightarrow{D}=\varepsilon {\varepsilon }_0\overrightarrow{E}\ \left(2.5\right),\]запишем:
\[\frac{D_1}{{\varepsilon }_0{\varepsilon }_1}sin\alpha =\frac{D_2}{{\varepsilon }_0{\varepsilon }_2}sin\beta \ \to \frac{D_1}{{\varepsilon }_1}sin\alpha =\frac{D_2}{{\varepsilon }_2}sin\beta \left(2.6\right).\] \[\frac{D_1}{{\varepsilon }_0{\varepsilon }_1}{\varepsilon }_1cos\alpha ={\varepsilon }_2\frac{D_2}{{\varepsilon }_0{\varepsilon }_2}cos\beta \to D_1cos\alpha =D_2cos\beta \left(2.7\right).\]Разделим (2.6) на (2.7), получим:
\[\frac{tg\alpha }{{\varepsilon }_1}=\frac{tg\beta }{{\varepsilon }_2}\to \frac{tg\alpha }{tg\beta }=\frac{{\varepsilon }_1}{{\varepsilon }_2}\ \left(2.8\right).\]Из уравнения (2.8) видно, что при переходе через границу из диэлектрика с меньшей диэлектрической проницаемостью в диэлектрик с большей проницаемостью угол увеличивается, то есть силовая линия удаляется от нормали. Значит, для нашего случая ${\varepsilon }_2>{\varepsilon }_1$.
Ответ: ${\varepsilon }_2>{\varepsilon }_1$.











