Потенциальная энергия жесткого диполя
Рассмотрим так называемый жесткий диполь -- это диполь, у которого расстояние между зарядами не изменяется ($l=const$). Определим, какова потенциальная энергия, которую имеет диполь во внешнем электростатическом поле. Если заряд $q$, который находится в точке поля с потенциалом $\varphi $, имеет потенциальную энергию равную:
то энергия диполя равна:
где ${\varphi }_+;{\varphi }_-$ - потенциалы внешнего поля в точках нахождения зарядов $q$ и $-q$. Потенциал электростатического поля убывает линейно, если поле однородно в направлении вектора напряженности поля. Направим ось X вдоль поля (рис.1). Тогда получим:
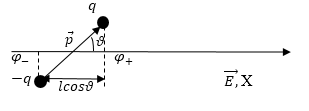
Рис. 1
Из рис. 1 видим, что изменение потенциала от ${\varphi }_+до\ {\varphi }_-$происходит на отрезке $\triangle x=lcos \vartheta$, поэтому:
Электрический момент диполя
Подставим (4) в (2), получим:
где $\overrightarrow{p}$=$q\overrightarrow{l}$ -- электрический момент диполя. Уравнение (6) не учитывает энергию взаимодействия зарядов диполя. Формула (6) получена при условии, что поле однородно, однако, она справедлива и для неоднородного поля.
Задание: Рассмотрите диполь, который находится в неоднородном поле, которое симметрично относительно оси X. Объясните, как поведет себя диполь в таком поле с точки зрения действующих на него сил.
Решение:
Пусть центр диполя лежит на оси X (рис.2). Угол между плечом диполя и осью X равен $\vartheta \ne \frac{\pi }{2}$. В нашем случае силы $F_1\ne F_2$.На диполь будет действовать вращательный момент и
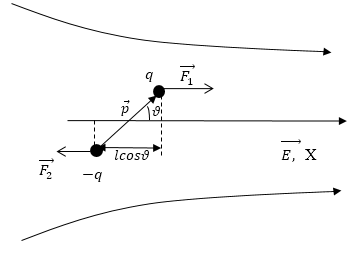
Рис. 2
сила, которая стремится переместить диполь по оси X. Чтобы найти модуль этой силы используем формулы:
\[F_x=-\frac{\partial W}{\partial x},\ F_y=-\frac{\partial W}{\partial y},\ F_z=-\frac{\partial W}{\partial z}(1.1).\]В соответствии с уравнением для потенциальной энергии диполя имеем:
\[W(x,y,z)=-pE(x,y,z)cos \vartheta \left(1.2\right),\]считаем, что $\vartheta=const$
Для точек оси X имеем:
\[F_y=-\frac{\partial W}{\partial y}=0,\ F_z=-\frac{\partial W}{\partial z}=0\] \[F_x=-\frac{\partial W}{\partial x}=p\frac{\partial E}{\partial x}cos \vartheta(1.3).\]При $\vartheta 0$, значит, диполь втягивается в область более сильного поля. При $\vartheta >\frac{\pi }{2}$ $F_x
Заметим, что если $-\frac{\partial W}{\partial x}=F_x$, производная от потенциальной энергии дает проекцию силы на соответствующую ось, то производная $-\frac{\partial W}{\partial \vartheta}=M_\vartheta$ дает проекцию вращательного момента на ось $?$:
\[-\frac{\partial W}{\partial \vartheta}=M_\vartheta=-pEsin \vartheta (1.4.)\]В формуле (1.4) минус означает, что момент стремится уменьшить угол меду электрическим моментом диполя и вектором напряженности поля. Диполь в электрическом поле стремится повернуться так, чтобы электрический момент диполя, был параллельно полю ($\overrightarrow{p}\uparrow \uparrow \overrightarrow{E}$). При $\overrightarrow{p}\uparrow \downarrow \overrightarrow{E}$ вращающий момент тоже будет равен нулю, но такое равновесие не устойчиво.
Задание: Два диполя находятся на расстоянии $r$ друг от друга. Их оси лежат на одной прямой. Электрические моменты равны соответственно: $p_1$ и $p_2$. Вычислите потенциальную энергию любого из диполей, которая будет соответствовать положению устойчивого равновесия.
Решение:
Система будет находиться в состоянии равновесия, когда диполи ориентированы, как показано на рис. 3, вдоль поля, противоположными по знаку зарядами друг к другу.
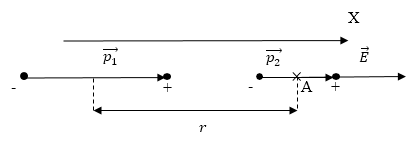
Рис. 3
Будем считать, что поле создаёт диполь с моментом $p_1$, будем искать потенциальную энергию диполя, который обладает электрическим моментом $p_2$ в точке поля (A) на расстоянии r от первого диполя. Примем, что плечи диполя малы по сравнению с расстоянием между диполями ($l\ll r$). Диполи можно будет принять за точечные (так считаем, что диполь с моментом $p_2\ находится\ в\ точке\ А$). Напряжённость поля, которое создает диполь на его оси в точке А по модулю равна (при $\varepsilon =1$):
\[E=\frac{p_1}{2\pi {\varepsilon }_0r^3}\left(2.1\right).\]Потенциальная энергия диполя с моментом $p_2$ в точке А может быть выражена формулой:
\[W=-p_2E\ \left(2.2\right),\]где мы учли, что векторы напряженности и электрического момента диполя сонаправлены в состоянии устойчивого равновесия. В таком случае потенциальная энергия второго диполя будет равна:
\[W=-p_2\frac{p_1}{2\pi {\varepsilon }_0r^3}\ \left(2.3\right).\]Ответ: Потенциальные энергии диполей будут равны по величине $W=-p_2\frac{p_1}{2\pi {\varepsilon }_0r^3}$.











