Уравнение вынужденных колебаний
Вынужденными колебаниями называют периодические изменения параметров, которые описывают систему под влиянием внешней силы. Для реализации вынужденных электрических колебаний в $RLC$ контуре в него включают переменную ЭДС (рис.1).
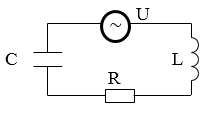
Рисунок 1.
В общем случае вынужденные колебания в таком контуре можно записать как:
где $L$ -- индуктивность, $R$ -- сопротивление, $C$ -- емкость, $U\left(t\right)$ -- внешнее воздействие.
Рассмотрим случай, когда в контур подается переменное напряжение ($U$) изменяющееся по гармоническому закону:
Тогда уравнение колебаний запишется в виде:
где ${\omega }_0=\frac{1}{\sqrt{LC}}$- собственная частота колебаний контура, $\beta =\frac{R}{2L}.$ По аналогии с механическими колебаниями можно записать частное решение данного уравнения как:
где $q_m=\frac{U_m}{\omega \sqrt{{R^2+\left(\omega L-1/\omega C\right)}^2}},\ tg\Psi=\frac{R}{\frac{1}{\omega C}-\omega L}$.
Как известно, общее решение неоднородного уравнения получают как сумму частного решения данного уравнения (в нашем случае это (4)) и общего решения соответствующего однородного уравнения. Так для уравнения:
общим решением является выражение:
Так как выражение (6) содержит множитель $e^{\left(-\beta t\right)}$, то при $t\to \infty ,\ $ $e^{\left(-\beta t\right)}\to 0,$ поэтому для установившихся колебаний решением уравнения (3) считают функцию (4).
Сила тока для установившихся вынужденных колебаний может быть записана как:
где $I_m={\omega q}_m$, $\varphi =\Psi-\frac{\pi }{2}$ -- сдвиг фаз между тока и приложенного напряжения. Соответственно:
Надо отметить, что выполняется равенство:
Выражение (9) означает, что сумма напряжений на каждом из элементов цепи в момент времени $t$ равна приложенному напряжению.
Резонанс
Появление сильных колебаний при частоте внешней силы равной (или почти равной) собственной частоте колебательного контура, называют резонансом. Суть явления заключается в том, что как бы одиночные «толчки» усиливают друг друга. В таком случае получается, что энергия, которая вкладывается в систему, является максимальной. Амплитуда колебаний нарастает до тех пор, пока увеличивающиеся силы трения (в среднем) за период толчка не станут компенсировать действие каждого «толчка». В этот момент устанавливается максимум энергии и максимум амплитуды.
Резонансной частотой для заряда (${\omega }_{qr}$) и напряжения (${\omega }_{Cr}$) на конденсаторе являются частоты, заданные уравнениями:
Резонансные кривые для заряда и напряжения на конденсаторе имеют одинаковый вид (рис.2).
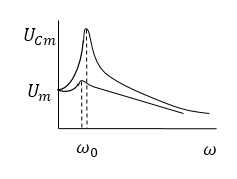
Рисунок 2.
Если $\omega =0$ кривые (рис.2) сходятся в одной точке, при этом напряжение на конденсаторе равно напряжению, которое возникает на нем при подключении источника:
Максимум резонансной кривой выше и острее, чем меньше коэффициент затухания (меньше $R$, больше $L$).
Кривые для силы тока изображены на рис. 3. Амплитудное значение силы тока максимально, если $\omega L-\frac{1}{\omega C}=0.\ $Частота силы тока при резонансе (${\omega }_{Ir}$):
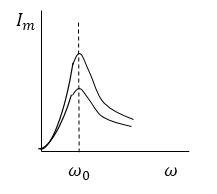
Рисунок 3.
Задание: Получите функции $U_R(t),U_C(t),U_L(t)$ в $RCL$ контуре, если приложенное напряжение задано уравнением: $U=U_m{cos \left(\omega t\right)\ }.$
Решение:
В качестве основы для решения задачи используем выражение:
\[I\left(t\right)={I_m cos\ }\left(\omega t-\varphi \right)\left(1.1\right).\]Исходя из (1.1) для напряжения на сопротивлении ($U_R$) в соответствии с законом Ома для участка цепи можно записать, что:
\[U_R\left(t\right)=RI\left(t\right)={{RI}_m cos\ }\left(\omega t-\varphi \right)\left(1.2\right).\]Используя закон изменения заряда в контуре, заданном в условии:
\[q=q_m{cos \left(\omega t-\Psi\right)\ }(1.3)\]найдем $U_C\left(t\right)$ как:
\[U_C\left(t\right)=\frac{q}{C}=\frac{q_m{cos \left(\omega t-\Psi\right)\ }}{C}=U_{mC}{cos \left(\omega t-\varphi -\frac{\pi }{2}\right)\ }\left(1.4\right),\]где $U_{mC}=\frac{q_m}{C}=\frac{I_m}{С\omega }.$ Напряжение на катушке индуктивности найдем как:
\[U_L=L\frac{dI}{dt}=-L\omega {I_m sin\ }\left(\omega t-\varphi \right)=U_{Lm}{cos \left(\omega t-\varphi +\frac{\pi }{2}\right)\ }\left(1.5\right).\]Ответ: $U_R\left(t\right)={{RI}_m cos\ }\left(\omega t-\varphi \right),\ U_C\left(t\right)=U_{mC}{cos \left(\omega t-\varphi -\frac{\pi }{2}\right)\ },\ U_L=U_{Lm}{cos \left(\omega t-\varphi +\frac{\pi }{2}\right).\ }$
Задание: Определите, во сколько раз напряжение на конденсаторе может превышать напряжение, которое приложено к $RLC$ контуру, если добротность контура равна $O$. Считать, что внешнее напряжение подчиняется гармоническому закону, затухание в контуре мало.
Решение:
Условие малости затухания для контура означает, что:
\[\beta \ll {\omega }_0(2.1)\]и резонансную частоту можно считать равной собственной частоте.
Напряжение на конденсаторе можно выразить как:
\[U_{mC}=\frac{q_m}{C}=\frac{U_m}{\omega C\sqrt{{R^2+\left(\omega L-\frac{1}{\omega C}\right)}^2}}\left(2.2\right)\]где $q_m=\frac{U_m}{\omega \sqrt{{R^2+\left(\omega L-1/\omega C\right)}^2}}$. Если при резонансе в нашем случае $\omega \approx {\omega }_0$, то максимальное напряжение на конденсаторе при резонансе равно ($U_{mCr}$):
\[U_{mCr}=\frac{U_m}{{\omega }_0C\sqrt{{R^2+\left({\omega }_0L-\frac{1}{{\omega }_0C}\right)}^2}}\ \approx \frac{U_m}{{\omega }_0RC}\left(2.3\right),\]где при малом затухании можно считать, что ${\omega }_0L-\frac{1}{{\omega }_0C}\approx 0$
Найдем отношение $\frac{U_{mCr}}{U_m}$, получим:
\[\frac{U_{mCr}}{U_m}=\frac{1}{{\omega }_0RC}=O\left(2.4\right),\]где $O=\frac{1}{R}\sqrt{\frac{L}{C}}$, ${\omega }_0=\frac{1}{\sqrt{LC}}$.
Ответ: $\frac{U_{mCr}}{U_m}=O.$











