Комплексная форма представления величин, которые характеризуют электрические колебания
Используем комплексную форму представления величин изменяющихся по гармоническому закону. Рассматривать будем установившийся режим. Если внешнее напряжение, подаваемое на цепь, изменяется по закону:
то сила тока должна изменяться как:
надо заметить, что величины $U{,U}_m,I{,I}_m$ в общем случае могут быть комплексными. Уравнение Ома для переменного тока в принятой форме обозначения имеет вид:
где импеданс $Z=R+i\left(\omega L-\frac{1}{\omega C}\right).$ В такой форме представления импеданс учитывает не только соотношение между амплитудами тока и напряжения, но и соотношение между их фазами. При этом:
Резонанс токов
В разветвленной цепи (рис.1) с двумя ветвями, одна из которых имеет индуктивность $L$, другая емкость ($C$) при равенстве $\omega L=\frac{1}{\omega C}$ наступает резонанс токов.
Допустим, что у нас имеется цепь, которая изображена на рис.1.
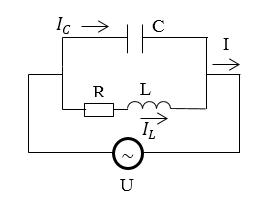
Рисунок 1.
Сила тока, которая течет в цепи, равна:
Запишем уравнение (5) в комплексном представлении:
Если
то получается, что сдвиг фаз между внешним напряжением и силой тока равен нулю. Разделим уравнение (7) на ${\omega }^2LC$, получим:
В том случае, если принять, что $\omega L\gg R$, то решением уравнения служит частота равная:
Частота ${\omega }0$ называется резонансной частотой. При резонансной частоте импеданс максимален, а амплитуда силы тока минимальна. Однако силы тока на емкости и индуктивности не являются минимальными. Векторная диаграмма сил токов для контура рис.1 изображена на рис.2.
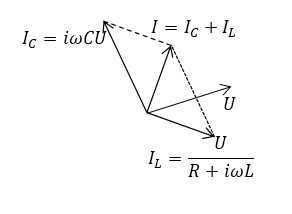
Рисунок 2.
В условиях приближения к резонансу диаграмма токов приобретает вид, который отображен на рис.3. При частоте, близкой к ${\omega }_0$ внутри контура циркулируют большие токи по сравнению с токами, которые подводят к данному контуру. Заряд внутри контура течет от емкости к индуктивности и наоборот. В контуре происходят колебания силы тока. В резонансе друг с другом находятся силы тока $I_C\ и\ I_L.$ Они компенсируют друг друга. Такой резонанс называют резонансом токов.
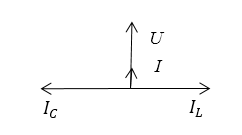
Рисунок 3.
Контур рис.1 выступает как резонансная система, которая совершает вынужденные колебания, под воздействием внешней силы. Колебания тока первым рассмотрел Томсон в 1853 г.
Отсутствие в цепи (или приближенное равенство нулю) активного сопротивления говорит о том, что энергия, запасённая в контуре, не рассеивается.
Одним из элементов электронного генератора является колебательный контур в состоянии резонанса токов. Резонанс токов используют в полосно -- заграждающих фильтрах.
Задание: Объясните, что происходит с энергией в контуре с параллельными емкостью и индуктивностью (рис.1). Если считать, что активное сопротивление равно нулю.
Решение:
В течение первой четверти периода напряжение на конденсаторе от нуля увеличивается до максимума ($U_{mC}$), при этом его энергия становится равна:
\[W_{mC}=\frac{CU_{mC}}{2}\left(1.1\right).\]В течение следующей четверти периода напряжение на конденсаторе уменьшается до нуля. Происходит освобождение энергии электрического поля.
За первую четверть периода колебаний в контуре ток в катушке от $I_{mL}$ уменьшается до нуля .Происходит освобождение энергии магнитного поля. За вторую четверть периода ток в катушке увеличивается до $I_{mL}$, энергия магнитного поля растет до величины:
\[W_{mL}=\frac{L{I^2}_{mL}}{2}\left(1.2\right).\]В течение первой четверти периода колебаний кинетическая энергия магнитного поля преобразуется в потенциальную энергию электрического поля, в течение следующей четверти периода идет обратный процесс. Обмен энергиями повторяется. При этом обмена энергией между контуром и источником питания нет, так как суммарный ток (ток в неразветвленной цепи равен нулю).
Задание: Чему равна ширина резонансной кривой, если в колебательный контур входят L, C?
Решение:
Ширина резонансной кривой ($2\triangle \omega $) определяется относительно квадрата амплитуды и ее можно определить как:
\[2\triangle \omega =\frac{{\omega }_0}{O}\left(2.1\right)\]Резонансную частоту выразим как:
\[{\omega }_0=\frac{1}{\sqrt{LC}}\left(2.2\right).\]Добротность контура $O$ равна:
\[O=\frac{1}{R}\sqrt{\frac{L}{C}}\left(2.3\right).\]Подставим правые части выражений (2.2) и (2.3) в (2.1), получим:
\[2\triangle \omega =\frac{R}{L}.\]Ответ: $2\triangle \omega =\frac{R}{L}.$













