Переходными процессами, возникающими в электрических цепях, называют явления (процессы), которые происходят в них после того как один из параметров испытал быстрое изменение. Например, включение и выключение ЭДС в цепи с сопротивлением и индуктивностью.
RC цепь
RC цепью называется электрическая цепь, которая состоит из конденсатора (конденсаторов) (емкость C), сопротивления (сопротивлений) (R) и источника ЭДС (рис.1). В такой цепи могут происходить только релаксационные непериодические процессы.
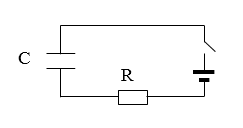
Рисунок 1.
Присутствие в цепи конденсатора исключает возможность существования в ней постоянного тока. Разность потенциалов между обкладками конденсатора полностью компенсирует действие сторонней ЭДС (источника). Переменный же ток в такой сети возможен благодаря переменному заряду на конденсаторе. Разность потенциалов на обкладках не компенсирует действия сторонней ЭДС, в результате чего поддерживается некоторая сила тока.
Закон Ома для RC цепи имеет вид:
где $q$ -- заряд на обкладке конденсатора, $\frac{q}{C}$ -- разность потенциалов между обкладками конденсатора, $U_0$- постоянное напряжение. Иногда уравнение (1) используют в виде:
Включение (выключение) постоянной ЭДС в RC цепи
Допустим, что постоянное напряжение ($U_0$) включают в момент времени, который мы принимаем за начальный ($t=0$). Из уравнения (1) следует, что:
Уравнение (2) при $t>0\ $запишем как:
Решением уравнения (4) при заданном начальном условии (3) является функция:
Из формулы (5) следует, что при $t\to \infty ,\ I\to 0.\ $ $I_{max}=\frac{U_0}{R}$. Время убывания силы тока ($\tau $) равно:
График функции $I\left(t\right)$ представлен на рис.2.
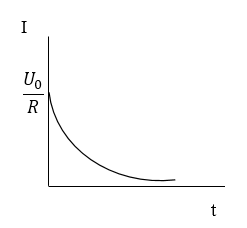
Рисунок 2.
Если в RC цепи емкость конденсатора велика, то ток после того как выключили источник постоянного напряжения может течь в цепи продолжительное время. Если в цепь включить лампу, то она сначала вспыхнет, за тем постепенно погаснет.
В момент времени, когда в RC цепи ток упал до нулевого значения, конденсатор зарядился максимально, разность потенциалов его обкладок равна величине сторонней ЭДС с противоположным знаком. Эти две величины компенсируют друг друга. Если каким-либо образом в этот момент выключить стороннюю ЭДС, то в цепи начнет течь ток, который возникает за счет некомпенсированной разности потенциалов на обкладках конденсатора. Начальная сила такого тока будет равна $\frac{U_0}{R}$, закон изменения тока. При этом закон изменения тока совпадет с функцией (5).
LC цепь
$LC$ цепью называют цепь, которая состоит из катушки индуктивности и емкости (рис.3).
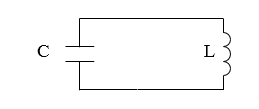
Рисунок 3.
В подобной цепи, не имеющей активного сопротивления, можно создать электрические колебания. Для этого сообщают обкладкам конденсатора начальный заряд или возбуждают ток в индуктивности (например, включая внешнее магнитное поле, которое пронизывает витки катушки). Допустим, что мы зарядили конденсатор. На обкладках конденсатора имеются заряды $q$ и $-q$. Между обкладками конденсатора появляется электрическое поле, энергия ($W_q$) которого равна:
Составили цепь из катушки и заряженного конденсатора. Конденсатор начнет разряжаться, в контуре возникнет ток. При этом энергия электрического поля уменьшается, энергия магнитного поля, которое порождается током, который течет через индуктивность, растет. Энергия магнитного поля ($W_m$) равна:
Так как активное сопротивление контура считается равным нулю, потерь энергии нет, то электрическая энергия постепенно переходит в магнитную, за тем магнитная переходит в электрическую. В момент, когда напряжение на конденсаторе равно нулю (следовательно, $W_q=0$), магнитная энергия максимальна, следовательно, ток в цепи максимален. Ток уменьшается, заряд растет. Весь цикл повторяется бесконечно.
Уравнение колебаний в контуре без активного сопротивления
Уравнение, которое описывает процесс изменения заряда в $LC$ контуре, имеет вид:
где $\frac{1}{LC}={\omega }_0$ -- собственная частота $LC$ -- контура. Решением уравнения (9) служит функция:
Из (10) видно, что заряд на обкладках конденсатора изменяется по гармоническому закону с частотой ${\omega }_0$.
Задание: Запишите функцию зависимости напряжения на конденсаторе от времени ($U(t)$) после замыкания ключа на рис. 4. Считать, что конденсатор был заряжен до напряжения $U_0$.
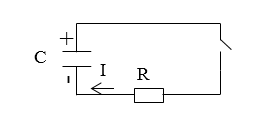
Рисунок 4.
Решение:
Используем второе правило Кирхгофа, запишем, что после того как ключ в цепи замкнули, выполняется равенство:
\[U_R+U_C=0\ \left(1.1\right),\]где $U_R$ -- напряжение на сопротивлении, $U_C$ -- напряжение на конденсаторе. При этом можно положить, что:
\[U_R=RI_R,\ I_C=C\frac{dU_C}{dt},\ I\left(t\right)=I_C=I_R\left(1.2\right),\]где $I_C,I_R$ токи, текущие через конденсатор и сопротивление. Используем выражения (1.2) преобразуем уравнение (1.1), получим:
\[\frac{dU_C}{dt}+\frac{1}{RC}U_C=0\left(1.3\right).\]Решение уравнения (1.3) запишем в виде:
\[U_C\left(t\right)=Aexp\left(-\frac{t}{RC}\right)\left(1.4\right).\]Постоянную А найден их начального условия задачи ($U_C\left(0\right)=U_0$), следовательно А=$U_0$.
Ответ: $U_C\left(t\right)=U_0exp\left(-\frac{t}{RC}\right).$
Задание: Приведите пример, как получить в примере 1 режим зарядки и разрядки конденсатора?
Решение:
Заданный режим можно получить, если в качестве источника постоянного напряжения использовать генератор прямоугольных импульсов (поставить его на место ключа рис. 4). При этом ЭДС источника ($\varepsilon (t$)) должна выглядеть как:
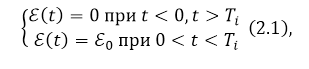
Рисунок 5.
где $T_i$ -- длительность импульса, причем это время должно быть существенно больше, чем время релаксации для того, чтобы напряжение на конденсаторе успело стать равным ${{\mathcal E}}_0$.












