Определение колебательного контура
В общем случае в колебательный контур включают сопротивление ($R$), конденсатор емкостью $C$, катушку индуктивности $L$, и источник сторонних ЭДС ($U$), тогда такой контур имеет вид, указанный на рис.1. При определенном соотношении параметров указанных элементов могут происходить колебания этого контура. В таком случае цепь называют колебательным контуром, он обладает определённой резонансной частотой. Ширину резонанса определяет такой параметр, как добротность системы, показывающий, во сколько раз энергия системы превосходит энергию потерь за изменение фазы колебаний в $1$ рад.
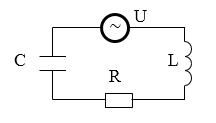
Рисунок 1. Колебательный контур. Автор24 — интернет-биржа студенческих работ
Существует два вида простых колебательных контуров:
- Контур, катушка и конденсатор в котором соединены параллельно, в этом случае возникает резонанс токов, при котором частота тока на катушке равна частоте тока на конденсаторе;
- Контур, в котором конденсатор подключён к катушке последовательно, в этом случае возникает резонанс напряжений, при котором система имеет частоту ${\omega }_0$.
Уравнение для тока в цепи имеет вид:
$IR=U-L\frac{dI}{dt}-\frac{q}{C}\left(1\right)$
или в другом виде:
$L\frac{d^2I}{dt^2}+R\frac{dI}{dt}+\frac{1}{C}I=\frac{dU}{dt}\left(2\right)$, где:
- $R$ — является сопротивлением прибора, включённого в цепь,
- $L$ — индуктивностью катушки,
- $C$ — значением емкости конденсатора,
- $U$ — ЭДС, возникающей в цепи.
Если цепь является $RC$ цепью или $RL$-цепью, то в ней существуют только непериодические процессы. В простейших случаях такие цепи описываются дифференциальными уравнениями первого порядка, например:
$\frac{dI}{dt}+\frac{1}{\tau }\left(I-I_{\infty }\right)=\frac{dU}{dt}\left(3\right),$
где $\tau $ — время релаксации, за которое сила тока по модулю уменьшится в $e$ раз. Решением такого уравнения является выражение:
$I\left(t\right)=I_{\infty }-\left(I_{\infty }-I\left(0\right)e^{-\frac{t}{\tau }}\right)\left(4\right).$
Собственные колебания
Собственными колебаниями называют колебания, которые совершаются за счет энергии, которую сообщили системе в начальный момент времени (т.е. нет постоянно действующего источника ЭДС) и предоставили самой себе.
Если собственные колебания вызваны наличием только квазиупругой силы, то они будут гармоническими.
Допустим, что источник ЭДС в колебательном контуре отсутствует, $\frac{dU}{dt}=0$, тогда уравнение (2) для колебательного контура примет вид:
$L\frac{d^2I}{dt^2}+R\frac{dI}{dt}+\frac{1}{C}I=0\left(5\right)$
Решение уравнения (5) может описывать свободные колебания контура при величине сопротивления, которое входит в состав контура $R
$I=A_0e^{\left(-\beta t\right)}{sin \left(\omega t+{\alpha }_0\right)\left(6\right),\ }$
где $\omega =\sqrt{\frac{1}{LC}-\frac{R^2}{4L^2}}$ — циклическая частота колебаний контура. $\beta =\frac{R}{2L}$ — коэффициент затухания (величина $\tau =\frac{1}{\beta }$ —время релаксации). (В уравнении может быть указан $cos$ вместо синуса — оба случая верны, мы помним, что эти функции имеют сдвиг на $\frac{\pi }{2}$). При $R >2\sqrt{\frac{L}{C}}$ изменение заряда не является колебаниями, разряд конденсатора называют апериодическим.
При $\beta =0$ в цепи осуществляются свободные незатухающие гармонические колебания, описываемые уравнением:
$L\frac{d^2I}{dt^2}+\frac{1}{C}I=0\ или\frac{d^2I}{dt^2}+{{\omega }_0}^2I=0\ \left(7\right),$
где ${\omega }_0=\frac{1}{\sqrt{LC}}$ — частота собственных гармонических колебаний контура.
Используем эту формулу для определения частоты и запишем решение уравнения (7) в виде:
$I(t)=I_0{sin \left({\omega }_0t+{\alpha }_0\right)\left(8\right),\ }$
где $I_0$ — амплитуда силы тока.
Если $\beta >0$, но потери энергии на сопротивлении малы, то колебания считают гармоническими.
В том случае, если в контуре присутствуют $L,R, C$ элементы и реализуется $\beta
Задание: Напишите функцию $U(t)$ для конденсатора, который изображен на схеме (рис.2). В цепи имеются конденсатор, емкость которого равна $C$, резистор с сопротивлением $R$ и генератор тока $I(t)$, который формирует ток вида:
$\left\{ \begin{array}{c} {I\left(t\right)=0\ при\ t0.} \end{array} \right.$

Рисунок 2. Схема цепи. Автор24 — интернет-биржа студенческих работ
Решение:
Суммарный ток в цепи $(I)$ в соответствии с первым правилом Кирхгофа можно записать как:
$I=I_R+I_C\left(1.1\right),$
где $I_R,I_C$ — токи, текущие через сопротивление и конденсатор, $I$ — ток генератора. Сопротивление и конденсатор соединены параллельно, следовательно:
$U_R=U_C=U\ \left(1.2\right).$
Используя формулы:
$I_R=\frac{U}{R},\ I_C=C\frac{dU}{dt}\left(1.3\right),$
подставим в (1.1), получим уравнение:
$C\frac{dU}{dt}+\frac{U}{R}=I\ \to \frac{dU}{dt}+\frac{1}{RC}\left(U-RI\right)=0\left(1.4\right).$
В качестве начального условия используем то, что напряжение на конденсаторе при $t=0$ равно нулю $(U(0)=0)$. Установившееся напряжение на конденсаторе будет равно:
$U'=I_0R\ \left(1.5\right).$
В качестве решения уравнения (1.4) получим выражение:
$U\left(t\right)=U'-\left(U'-U\left(0\right)\right){exp \left(-\frac{t}{RC}\right)\ }=I_0R\left(1-{exp \left(-\frac{t}{RC}\right)\ }\right).$
Ответ: $U\left(t\right)=I_0R\left(1-{exp \left(-\frac{t}{RC}\right)\ }\right).$
Задание: Какова зависимость напряжения на конденсаторе от времени $(U(t))$ после того как замкнули ключ на схеме рис.3? Учесть, что сопротивление резистора равно $R$, конденсатор емкостью $C$ изначально не заряжен, в цепь включен генератор постоянного напряжения ($\mathcal E$).
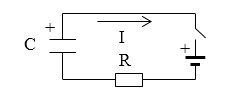
Рисунок 3. Схема цепи. Автор24 — интернет-биржа студенческих работ
Решение:
По второму правилу Кирхгофа запишем:
$U_C+U_R={\mathcal E}\ \left(2.1\right),$
где $U_C,U_R$ напряжения на конденсаторе и сопротивлении. Еще мы знаем, что:
$U_R=RI_R,\ I_C=C\frac{dU_C}{dt}\left(2.2\right).$
На схеме все элементы цепи соединены последовательно, значит:
$I\left(t\right)=I_R=\ I_C\left(2.3\right).$
В соответствии с избранным направлением обхода контура и уравнениями (2.1)- (2.3) имеем:
$U_C+RC\frac{dU_C}{dt}={\mathcal E}\to \frac{dU_C}{dt}+\frac{1}{RC}\left(U_C-{\mathcal E}\right)\left(2.4\right).$
В соответствии с заданными начальными условиями запишем:
$U_C\left(0\right)=0\ \left(2.5\right).$
Решением уравнения (2.4) будет функция:
$U_C\left(t\right)={\mathcal E}\left(1-e^{-\frac{t}{RC}}\right).$
Ответ: $U_C\left(t\right)={\mathcal E}\left(1-e^{-\frac{t}{RC}}\right).$











