Определение связности контуров. Уравнения для системы проводников
Два контура называют связанными, если между ними существует электрическая связь, из-за которой часть энергии одного контура может передаваться во второй и наоборот.
Любой из контуров, по которому течет переменный ток, является источником переменного магнитного поля. В соответствии с законом электромагнитной индукции это поле создает в других контурах, которые находятся в этом поле ЭДС, которая изменяет силу токов, находящихся во внешнем магнитном поле. Получается, что контуры связаны между собой через электромагнитную индукцию.
Полный магнитный поток, который пронизывает контур с номером $k$ можно определить как:
где $L_{kk}$- индуктивность контура $k$. $L_{ki}$ -- взаимная индуктивность контуров $k$- го и $i$-го. Количество проводников при этом равно $N$. Если емкости в цепях считать равными нулю, то с учетом электромагнитной индукции сила тока в контуре с номером $k$ можно найти из уравнения:
где $U_k$ -- сторонняя движущая сила в контуре $k$. Если использовать (1), подставить его в (2), то получим:
где $k=1,2,...,N$.
Колебания, связанные через индуктивность
Пусть мы имеем систему из двух $LC$ контуров, которые связаны между собой через индуктивность (рис.1). Допустим, что сопротивления таких контуров мало ($R\approx 0$). Внешние силы на систему не действуют, значит, мы имеем дело со свободными колебаниями. Понятно, что колебания, которые происходят в одном контуре, влияют на колебания в другом контуре. Подобные колебания называют связанными.
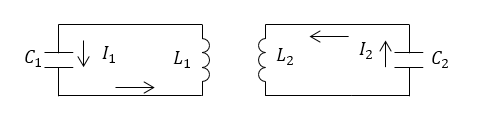
Рисунок 1.
Колебания, связанные через индуктивность описываются дифференциальными уравнениями:
Или, что то же самое:
Уравнения (5) представим в виде:
где мы вводим обозначения:
Первое частное решение системы уравнений (3) имеет вид:
Второе частное решение системы (6):
где
Общее решение системы (6) линейная комбинация частных решений:
где $C_1$ и $C_2$ -- произвольные комплексные постоянные, которые находятся из начальных условий.
Колебания, связанные через емкость
Рассмотрим колебательные контуры с емкостной связью (рис.2).
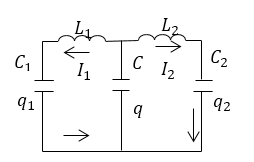
Рисунок 2.
В случае, представленном на рис.2 колебания в такой системе описываются равнениями:
Если учесть, что:
то уравнение (12) можно преобразовать к виду:
где мы вводим обозначения:
Если сравнить системы уравнений (14) и (6), очевидно, что данные системы уравнений однотипны. Это линейные дифференциальные уравнения второго порядка с постоянными коэффициентами. Следовательно, система (14) решается аналогично системе (6).
Задание: Два одинаковых контура связаны через емкости. Найдите частоты (${\omega }_{1\ }и\ {\omega }_{2\ }$), с которыми совершают колебания каждый из контуров.
Решение:
Уравнения, описывающих колебания контуров, связанных через емкости:
\[{\ddot{I}}_1+a_{11}I_1+a_{12}I_2=0,\ {\ddot{I}}_2+a_{21}I_1+a_{22}I_2=0\left(1.1\right),\]где:
\[a_{11}=\frac{1}{L_1}(\frac{1}{C_1}+\frac{1}{C}),\ a_{12}=\frac{1}{L_1C},\ a_{21}=\frac{1}{L_2C},\ a_{22}=\frac{1}{L_2}(\frac{1}{C_2}+\frac{1}{C}).\]Общее решение системы (1.1):
\[I_1={C_1e}^{i{\omega }_1t}+{C_2e}^{i{\omega }_2t},\ I_2=h_1e^{i{\omega }_1t}+h_2e^{i{\omega }_2t}\left(1.2\right),\]где $h_1=\frac{{\omega }^2_1-a_{11}}{a_{12}}=\frac{a_{21}}{{\omega }^2_1-a_{22}},\ h_2=\frac{{\omega }^2_2-a_{11}}{a_{12}}=\frac{a_{21}}{{\omega }^2_2-a_{22}}\ $
Если контуры одинаковы, то для коэффициентов можно записать соотношения:
\[a_{11}=a_{22},\ a_{12}=a_{21}\left(1.3\right).\]Тогда мы имеем:
\[{\omega }^2_1=a_{11}+a_{12},\ \omega^2_2=a_{11}-a_{12},\ h_1=1,\ h_2=-1\left(1.4\right).\]Следовательно:
\[{\omega }^2_1=\frac{1}{L_1}\left(\frac{1}{C_1}+\frac{2}{C}\right),\ \omega^2_2=\frac{1}{L_1C_1}.\]Ответ: ${\omega }_1=\sqrt{\frac{1}{L_1}\left(\frac{1}{C_1}+\frac{2}{C}\right)},\ \omega_2=\sqrt{\frac{1}{L_1C_1}}.$
Задание: Допустим, что в симметричном случае связь между контрами слабая. Какое явление может возникать в двух связанных контурах?
Решение:
Для уравнения, которое описывает колебания слова «слабая связь между контурами» означает, что коэффициенты $a_{12}$=$a_{21}$ малы. Это означает, что частоты ${\omega }_1\ и\ \omega_2$ приблизительно равны, и близки к собственной частоте контура (${\omega }_0$), которая равна:
\[{\omega }_0=\sqrt{a_{11}}\left(2.1\right).\]На протяжении нескольких колебаний токи (в случае емкостной связи) изменяются так, как будто связи между контурами не существует. Наличие слабой связи приводит к возникновению биений. Когда амплитуда одного тока проходит через максимум, другая равна нулю и наоборот.











