
При одновременном действии на одно тело нескольких сил тело движется с ускорением, являющимся векторной суммой ускорений, которые бы возникли под действием каждой силы в отдельности. Действующие на тело силы, приложенные к одной точке, складываются по правилу сложения векторов.
Векторная сумма всех сил, одновременно действующих на тело, называется равнодействующей силой и определяется правилом векторного сложения сил: $\overrightarrow{R}={\overrightarrow{F}}_1+{\overrightarrow{F}}_2+{\overrightarrow{F}}_3+\dots +{\overrightarrow{F}}_n=\sum^n_{i=1}{{\overrightarrow{F}}_i}$.
Равнодействующая сила оказывает на тело такое же действие, как сумма всех приложенных к нему сил.
Для сложения двух сил используется правило параллелограмма (рис.1):
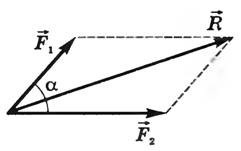
Рисунок 1. Сложение двух сил по правилу параллелограмма
При этом модуль суммы двух сил находим по теореме косинусов:
\[\left|\overrightarrow{R}\right|=\sqrt{{\left|{\overrightarrow{F}}_1\right|}^2+{\left|{\overrightarrow{F}}_2\right|}^2+2{\left|{\overrightarrow{F}}_1\right|}^2{\left|{\overrightarrow{F}}_2\right|}^2{cos \alpha \ }}\]Если нужно сложить более двух сил, приложенных в одной точке, то пользуются правилом многоугольника:~ из конца первой силы проводят вектор, равный и параллельный второй силе; из конца второй силы -- вектор, равный и параллельный третьей силе и так далее.
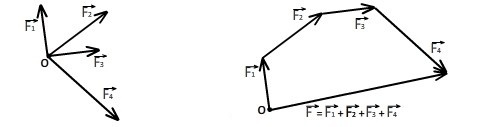
Рисунок 2. Сложение сил по правилу многоугольника
Замыкающий вектор, проведённый из точки приложения сил к концу последней силы, по величине и направлению равен равнодействующей. На рис.2 это правило проиллюстрировано на примере нахождения равнодействующей~~четырёх сил ${\overrightarrow{F}}_1,\ {\overrightarrow{F}}_2,{\overrightarrow{F}}_3,{\overrightarrow{F}}_4$. Заметим, что при этом складываемые векторы не обязательно должны принадлежать одной плоскости.
Результат действия силы на материальную точку зависит только от ее модуля и направления. Твердое же тело имеет определенные размеры. Поэтому одинаковые по модулю и направлению силы вызывают различные движения твердого тела в зависимости от точки приложения. Прямая, проходящая через вектор силы, называется линией действия силы.
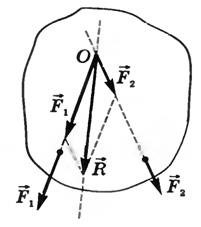
Рисунок 3. Сложение сил, приложенных к разным точкам тела
Если силы приложены к разным точкам тела и действуют не параллельно друг другу, то равнодействующая приложена к точке пересечения линий действия сил (рис.3).
Точка находится в равновесии, если векторная сумма всех сил, действующих на нее, равна нулю: $\sum^n_{i=1}{{\overrightarrow{F}}_i}=\overrightarrow{0}$. В этом случае равна нулю и сумма проекций этих сил на любую ось координат.
Замену одной силы двумя, приложенными в той же точке и производящими на тело такое же действие, как и эта одна сила, называют разложением сил. Разложение сил производят, как и их сложение, по правилу параллелограмма.
Задача разложения одной силы (модуль и направление которой известны) на две, приложенные в одной точке и действующие под углом друг к другу, имеет однозначное решение в следующих случаях, если известны:
- направления обеих составляющих сил;
- модуль и направление одной из составляющих сил;
- модули обеих составляющих сил.
Пусть, например, мы хотим разложить силу $F$ на две составляющие, лежащие в одной плоскости с F и направленные вдоль прямых а и b (рис.4). Для этого достаточно из конца вектора, изображающего F, провести две прямые, параллельные a и b. Отрезки $F_A$ и $F_B$ изобразят искомые силы.
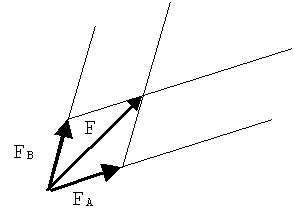
Рисунок 4. Разложение вектора силы по направлениям
Другой вариант этой задачи - нахождение одной из проекций вектора силы по заданным векторам силы и второй проекции. (рис.5 а).
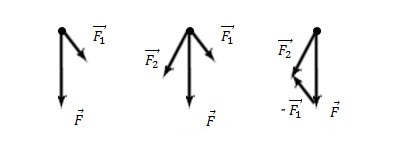
Рисунок 5. Нахождение проекции вектора силы по заданным векторам
Задача сводится к построению параллелограмма по диагонали и одной из сторон, известному из планиметрии. На рис.5б построен такой параллелограмм и указана искомая составляющая ${\overrightarrow{F}}_2$ силы ${\overrightarrow{F}}$.
Второй способ решения: прибавить к силе силу, равную - ${\overrightarrow{F}}_1$ (рис.5в).В результате получим искомую силу ${\overrightarrow{F}}_2$.
Три силы~${\overrightarrow{F}}_1=1\ Н;;\ {\overrightarrow{F}}_2=2\ Н;;\ {\overrightarrow{F}}_3=3\ Н$ приложены к одной точке , лежат в одной плоскости (рис.6 а) и составляют углы~ с~ горизонталью $\alpha =0{}^\circ ;;\beta =60{}^\circ ;;\gamma =30{}^\circ $соответственно. Найдите равнодействующую этих сил.
Решение
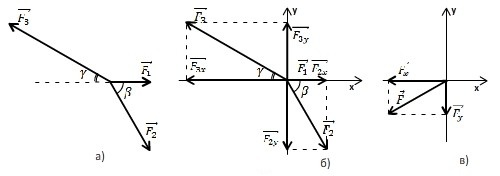
Проведём две взаимно перпендикулярные оси ОХ и OY так, чтобы ось ОХ совпадала с горизонталью, вдоль которой направлена сила ${\overrightarrow{F}}_1$. Спроецируем данные силы на оси координат (рис.6 б). Проекции $F_{2y}$ и $F_{2x}$ отрицательны. Сумма проекций сил на ось ОХ равна проекции на эту ось равнодействующей: $F_1+F_2{cos \beta \ }-F_3{cos \gamma \ }=F_x=\frac{4-3\sqrt{3}}{2}\approx -0.6\ H$. Аналогично, для проекций на ось OY: $-F_2{sin \beta \ }+F_3{sin \gamma =F_y=\ }\frac{3-2\sqrt{3}}{2}\approx -0.2\ H$. Модуль равнодействующей определяется по теореме Пифагора: $F=\sqrt{F^2_x+F^2_y}=\sqrt{0.36+0.04}\approx 0,64\ Н$. Направление равнодействующей определим с помощью угла между равнодействующей и осью (рис.6 в): $tg\varphi =\frac{F_y}{F_x}=\ \frac{3-2\sqrt{3}}{4-3\sqrt{3}}\approx 0.4$
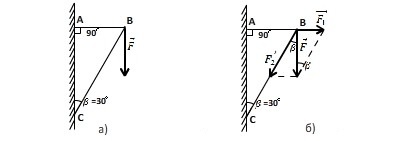
Сила $F = 1kH$ приложена в точке В кронштейна и направлена вертикально вниз (рис.7а). Найдите составляющие этой силы по направлениям стержней кронштейна. Необходимые данные указаны на рисунке.
Решение
Дано:
F = 1 кН = 1000Н
${\mathbf \beta }$ = $30^{\circ}$
${\overrightarrow{F}}_1,\ {\overrightarrow{F}}_2$ - ?
Пусть стержни прикреплены к стене в точках A и C. Разложение силы ${\overrightarrow{F}}$ на составляющие вдоль направлений АВ и ВС представлено на рис.7б. Откуда видно, что $\left|{\overrightarrow{F}}_1\right|=Ftg\beta \approx 577\ H;\ \ $
\[\left|{\overrightarrow{F}}_2\right|=F{cos \beta \ }\approx 1155\ H. \]Ответ: $\left|{\overrightarrow{F}}_1\right|$=577 Н; $\left|{\overrightarrow{F}}_2\right|=1155\ Н$











