Сила сопротивления при движении в вязкой среде
В отличие от сухого вязкое трение характерно тем, что сила вязкого трения обращается в нуль одновременно со скоростью. Поэтому, как бы ни была мала внешняя сила, она может сообщить относительную скорость слоям вязкой среды.
Следует иметь в виду, что, помимо собственно сил трения, при движении тел в жидкой или газообразной среде возникают так называемые силы сопротивления среды, которые могут быть гораздо значительнее, чем силы трения.
Правила поведения жидкости и газа в отношении трения не различаются. Поэтому все сказанное ниже относится в равной степени и к жидкостям, и к газам.
Сила сопротивления, возникающая при движении тела в вязкой среде обладает определенными свойствами:
- отсутствует сила трения покоя - например, человек может сдвинуть с места плавающий многотонный корабль, просто потянув за канат;
- сила сопротивления зависит от формы движущегося тела - корпус подводной лодки, самолёта или ракеты имеет обтекаемую сигарообразную форму --- для уменьшения силы сопротивления, наоборот, при движении полусферического тела вогнутой стороной вперёд сила сопротивления очень велика (пример --- парашют);
- абсолютная величина силы сопротивления существенно зависит от скорости.
Сила вязкого трения
Изложим закономерности, которым подчиняются силы трения и сопротивления среды совместно, причём условно будем называть суммарную силу силой трения. Вкратце эти закономерности сводятся к следующему - величина силы трения зависит:
- от формы и размеров тела;
- состояния его поверхности;
- скорости по отношению к среде и от свойства среды, называемого вязкостью.
Типичная зависимость силы трения от скорости тела по отношению к среде показана графически на рис. 1.~
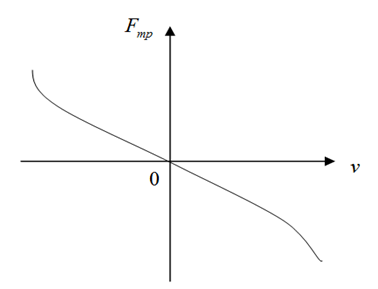
Рисунок 1. График зависимости силы трения от скорости по отношению к среде
При малых скоростях движения сила сопротивления прямо пропорциональна скорости и сила трения растет линейно со скоростью:
$F_{mp} =-k_{1} v$ , (1)
где знак «-» означает, что сила трения направлена в сторону, противоположную скорости.
При больших скоростях линейный закон переходит в квадратичный т.е. сила трения начинает расти пропорционально квадрату скорости:
$F_{mp} =-k_{2} v^{2}$ (2)
Например, при падении в воздухе зависимость силы сопротивления от квадрата скорости имеет место уже при скоростях около нескольких метров в секунду.
Величина коэффициентов $k_{1} $ и $k_{2}$ (их можно назвать коэффициентами трения) в сильной степени зависит от формы, и размеров тела, состояния его поверхности и от вязких свойств среды. Например, для глицерина они оказываются гораздо большими, чем для воды. Так, парашютист при затяжном прыжке не набирает скорость безгранично, а с определённого момента начинает падать с установившейся скоростью, при которой сила сопротивления становится равна силе тяжести.
Значение скорости, при которой закон (1) переходит в (2), оказывается зависящим от тех же причин.
Два металлических шарика, одинаковых по размеру и различных по массе, падают без начальной скорости с одной и той же большой высоты. Какой из шариков быстрее упадёт на землю --- лёгкий или тяжёлый?
Дано: $m_{1} $, $m_{2} $, $m_{1} >m_{2} $.
Решение.
Шарики при падении не набирают скорость безгранично, а с определённого момента начинают падать с установившейся скоростью, при которой сила сопротивления (2) становится равна силе тяжести:
\[F_{mp} =k_{2} v^{2} =mg.\]Отсюда установившаяся скорость:
\[v^{2} =\frac{mg}{k_{2} } .\]Из полученной формулы следует, что у тяжёлого шарика установившаяся скорость падения больше. Значит, он дольше будет набирать скорость и потому быстрее достигнет земли.
Ответ: Тяжелый шарик быстрее достигнет земли.
Парашютист, летящий до раскрытия парашюта со скоростью $35$ м/с, раскрывает парашют, и его скорость становится равной $8$ м/с. Определите, какой примерно была сила натяжения строп при раскрытии парашюта. Масса парашютиста $65$ кг, ускорение свободного падения $10 \ м/с^2.$ Принять, что $F_{mp}$ пропорциональна $v$.
Дано: $m_{1} =65$кг, $v_{1} =35$м/с, $v_{2} =8$м/с.
Найти: $T$-?
Решение:
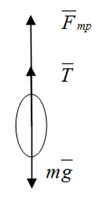
Рисунок 2.
До раскрытия парашюта парашютист имел
постоянную скорость $v_{1} =35$м/с, значит ускорения парашютиста было равно нулю.
Запишем второй закон Ньютона:
\[0=mg-kv_{1} \]Отсюда:
\[k=\frac{mg}{v_{1} } .\]После раскрытия парашюта парашютист имел постоянную скорость $v_{2} =8$м/с.
Второй закон Ньютона для этого случая будет выглядеть следующим образом:
\[0=mg-kv_{2} -T.\]Тогда искомая сила натяжения строп будет равна:
$T=mg(1-\frac{v_{2} }{v_{1} } )\approx 500$ Н.
Ответ: $T=500$Н.











