Система отсчета. Системы координат
Под движением материальной точки в пространстве понимают изменение ее положения относительно некоторых тел с течением времени. В связи с этим можно говорить только о движении в некоторой системе отсчета.
Сами по себе точки пустого пространства неразличимы между собой, поэтому говорить о той или иной точке пространства можно, если в ней находится материальная точка. Ее положение и определяется относительно тела отсчета с помощью измерений, для чего с телом (телами) отсчета жестко связывается некоторая система координат; в ней и измеряются пространственные координаты. Например, на поверхности Земли это географическая широта и долгота точки.
В теоретических рассуждениях часто наиболее удобна декартова прямоугольная система координат, в которой положение точки определяется радиус-вектором $\overline{r}$ с тремя проекциями $x,y,z$ -- координатами точки. Но возможно и использование других систем координат, например:
- сферической, где положение точки и ее радиус-вектор определены координатами $r,\vartheta ,\varphi $;
- цилиндрической: с координатами $p,z,\alpha $;
- на плоскости - полярной: $r,\varphi $.
В теоретических рассуждениях часто не принимают во внимание реальную систему отсчета, сохраняя только систему координат, которая и служит математической моделью системы отсчета, применяемой при измерениях на практике.
Кинематическое уравнение движения материальной точки
Итак, в любой системе отсчета и системе координат имеется возможность определить координаты материальной точки в любой момент времени.
Если положение материальной точки в каждый момент времени определено в данной системе отсчета, то движение ее задано или описано.
Это задание достигается в виде кинематического уравнения движения:
$\overline{r}=\overline{r}(t)$ (1)
Аналитически положение точки всегда определяется совокупностью трех независимых между собой чисел. Этот факт выражают словами: свободная точка имеет три степени свободы движения.
Движение точки согласно уравнению (1) полностью определено, если указано ее положение в любой момент времени $t$. Для этого достаточно задать декартовы координаты точки как однозначные и непрерывные функции времени:
$x(t)=x$, $y(t)=y$, $z(t)=z$. (2)
Прямоугольные декартовы координаты $x,y,z$ являются проекциями радиус-вектора $\overline{r}$, проведенного в точку из начала координат, т.е.:
Длина и направление вектора $\overline{r}$находятся из известных соотношений:
Здесь, $\alpha ,\beta ,\gamma $ - углы, образованные радиус-вектором с координатными осями.
Равенства (2) являются кинематическими уравнениями движения материальной точки в декартовых координатах. Но уравнения могут быть записаны в любой другой системе координат, связанной с декартовой взаимно однозначным преобразованием. При движении точки в плоскости Оху часто бывает удобно пользоваться полярными коордиинатами $r,\varphi $, связанными с декартовыми преобразованием:
В этом случае кинематические уравнения движения точки имеют следующий общий вид:
$r=r(t),\varphi =\varphi (t)$. (3)
В криволинейных координатах $q_{1} ,q_{2} ,q_{3} $ связанных с декартовыми преобразованием:
$x=x(q_{1} ,q_{2} ,q_{3} )$, $y=y(q_{1} ,q_{2} ,q_{3} )$, $z=z(q_{1} ,q_{2} ,q_{3} )$, (4)
кинематические уравнения движения точки запишутся так:
$q_{1} =q_{1} (t),q_{2} =q_{2} (t),q_{3} =q_{3} (t)$. (5)
(Это могут быть сферические, цилиндрические и другие координаты).
Годограф радиус-вектора точки, т.е. кривая, описываемая концом вектора $\overline{r}$при движении точки, совпадает с траекторией движения этой точки. Уравнение траектории в параметрической форме, когда параметром служит время $t$, дано кинематическими уравнениями движения (2), (5). Для получения уравнения траектории в координатной форме достаточно исключить из кинематических уравнений время.
Движение точки может быть определено по-другому: заданием траектории и мгновенным положением точки на ней. Положение точки на кривой определяется указанием только одной величины -- расстояния, измеряемого вдоль кривой от некоторой начальной точки. При этом должно быть указано положительное направление кривой. Тогда мгновенное положение точки на заданной кривой определяется функцией:
Это уравнение является уравнением движения точки по траектории. Такой способ задания движения называется естественным или траекторным.
Координатный и естественный способы задания движения точки физически (в смысле фиксации ее положения в пространстве)
эквивалентны. Что же касается математической стороны дела, то в одних задачах оказывается проще применение координатного, а в другом -- естественного метода.
Закон движения точки по траектории может быть задан аналитически, графически или в виде таблицы. Оба последних способа широко применяются на транспорте (например, графики и расписания движения поездов).
Уравнение движения материальной точки имеет вид $x=0,4t^{2} $. Написать формулу зависимости $v_{x} (t)$ и построить график зависимости скорости точки от времени. Показать на графике площадь, численно равную пути, пройденному точкой за 4 секунды, и вычислить этот путь. \end{enumerate}
Дано: $x=0,4t^{2} $, $t=4$с.
Найти: $v_{x} (t)$, $S$-?
Решение: Зависимость скорости от времени имеет вид:
\[v_{x} =v_{0x} +a_{x} t.\]Запишем уравнение зависимости координаты от времени и сравним его с данным:
\[x=x_{0} +v_{0x} t+\frac{a_{x} t^{2} }{2} , x=0,4t^{2} .\]Из сравнения видно, что $x_{0} =0$, $v_{0x} =0$, $a_{x} =0,8$м/с2.
Подставим полученные данные в уравнение скорости и получим:
\[v_{x} =0,8t.\]Определим точки и построим график:
\[v_{x} =0,t=0; v_{x} =4,t=5.\]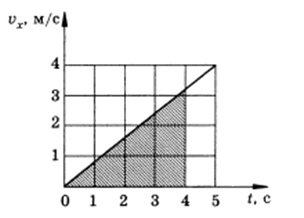
Рисунок 1.
Путь, пройденный телом, численно равный площади фигуры, ограниченной графиком и может быть найден по следующей формуле:
$S=0,4t^{2} =6,4$м.
Ответ: $S=6,4$ м.











